4．平行四边形的一组对角的和为280°，则其相邻的两个内角分别为_______．

3．平行四边形的一个外角等于60°，那么该平行四边形两个相邻内角的比为( )．

　　 (A)2：1　　 (B)3：1　　 (C)4：1　　 (D)5：1

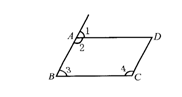
2．如图，在ABCD中，下列各式不一定正确的是(　 )．

　 (A)∠1+∠2=180°；(B)∠2+∠3=180°；

(C)∠3+∠4=180°；(D)∠2+∠4=180°

1．在ABCD中，

　(1)若∠A=30°，则∠B=______，∠C=________，∠D=________．

　(2)若∠A：∠B=1：2，则∠A=______，∠B=_______，∠D=_______．

　 (3)若∠A-∠B=40°，则∠A=______，∠B=_______．

　 (3)若∠A+∠C=90°，则∠D=________．

5．2 平行四边形 同步练习

解题示范

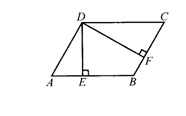
例　 在ABCD中，DE⊥AB于点E，DF⊥BC于点F，且∠ADE+∠CDF=60°，求∠EDF的度数．

　　 审题　 在ABCD中，已知条件有∠AED=∠CFD=90°，∠ADE+∠CDF=60°，结论是求∠EDF的度数．

　　 方案　 因为∠DEB=∠DFB=90°，所以要求得∠EDF的度数，只要求出∠B即可．而∠B+∠C=180°，故只需知道∠C的度数即可．根据平行四边形的对角相等，得∠A=∠C．又∠AED=∠CFD=90°，在△ADE和△CDF中，易求∠ADE=∠CDF=30°，可求得∠A=∠C=60°．

实施　 ∵四边形ABCD是平行四边形，

∴∠A=∠C，AD∥BC．

　　 ∴∠A+∠B=180°．

∵DE⊥AB，

∴∠A+∠ADE=90°．

同理∠C+∠CDF=90°．

　　 ∴∠ADE=∠CDF．

又∠ADE+∠CDF=60°，

∴∠ADE=∠CDF=30°，

∴∠A=60°．

　　 ∴∠B=180°-∠A=180°-60°=120°．

　　 在四边形DEBF中，∠DEB+∠B+∠BFD+∠FDE=360°，

　　 ∴∠EDF=360°-90°-120°-90°=60°．

　　 反思　 (1)在平行四边形中，运用对角相等，邻角互补是解决角问题的重要条件．(2)在解决几何问题时，要善于挖掘图形的典型特征．

课时训练

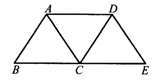
15．如图所示，已知在△ABC中，AB=AC=5，BC=6，将△ABC沿BC所在直线向右平移6个单位，得到△DCE，连结AD．

　　 (1)请找出图中所有的平行四边形．(2)求四边形ABED的面积．

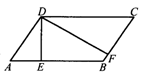
14．如图所示，在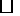ABCD中，DE⊥AB于E，DF⊥BC于F，若∠A=55°，求∠EDF的度数．

[综合提高]

13．如图所示，在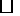ABCD中，点E，F分别在BC，AD上，AE∥CF，求证：∠AFC=∠AEC．

12．在平行四边形中，已知一个角是它的邻角的3倍，求这个角的度数．

11．如图3所示，在△ABC中，D，E，F分别是AB，BC，AC上的点，且DE∥AC，EF∥AB，DF∥BC，则图中平行四边形共有(　 )

　　 A．1个　　 B．2个　　 C．3个　　 D．4个

[应用拓展]