
题目列表(包括答案和解析)
1.  的解集是___________,
的解集是___________,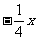 ≤-8的解集是___________。
≤-8的解集是___________。
9、某地区一种商品的需求量y1(万件),供应量y2(万件)与价格(元/件)分别近似满足下列函数关系式: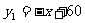 ,
,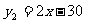 .需求量为0时,即停止供应. 当
.需求量为0时,即停止供应. 当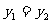 时,该商品的价格称为稳定价格,需求量称为稳定需求量.
时,该商品的价格称为稳定价格,需求量称为稳定需求量.
(1)求该商品的稳定价格和稳定需求量;
(2)当价格在什么范围时,该商品的需求量低于供应量?
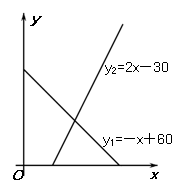 (3)当需求量高于供应量时,政府常通过对供应方提供价格补贴来提高供货价格,以提高供应量. 若要使稳定需求量增加2万件,政府应对每件商品提供多少元补贴,才能使供应量等于需求量?
(3)当需求量高于供应量时,政府常通过对供应方提供价格补贴来提高供货价格,以提高供应量. 若要使稳定需求量增加2万件,政府应对每件商品提供多少元补贴,才能使供应量等于需求量?
8、某公司为了扩大经营,决定购进6台机器用于生产某种活塞.现有甲、乙两种机器供选择,其中每种机器的价格和每台机器日生产活塞的数量如下表所示.经过预算,本次购买机器所耗资金不能超过34万元.
|
|
甲 |
乙 |
|
价格(万元/台) |
7 |
5 |
|
每台日产量(个) |
100 |
60 |
(1)按该公司要求可以有几种购买方案?
(2)若该公司购进的6台机器的日生产能力不能低于380个,那么为了节约资金应选择哪种方案?
7、已知,一次函数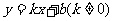 ,当
,当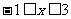 时,
时,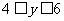 ,求
,求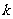 ,
,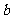 的值。
的值。
6、某软件公司开发出一种图书管理软件,前期投入的开发广告宣传费用共用50000元,且每售出一套软件,软件公司还需支付安装调试费用200元。
(1)试写出总费用(元)与销售套数(套)之间的函数关系;
(2)如果每套定价700元,软件公司至少要售出多少套软件才能确保不亏本?
5、某学校组织三好学生去野营,若每个帐篷住6人,则有20人没地方住;若每个帐篷住9人,则还有一个帐篷里不空也不满,问:有多少个帐篷?多少学生?
4、某商店在一次促销活动中规定:消费者消费满200元或超过200元就可享受打折优惠.一名同学为班级买奖品,准备买6本影集和若干支钢笔.已知影集每本15元,钢笔每支8元,问他至少买多少支钢笔才能打折?
3、解不等式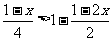 ,并写出它的最大整数解.
,并写出它的最大整数解.
2、解不等式组,并将解集在数轴上表示出来。
(1) (2)
(2)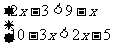
1、解不等式
(1) (2)
(2)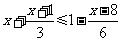
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com