3．若(x-3)是kx⁴+10x-192的一个因式，求k的值．

2．在实数范围内分解

(1)x⁴-11x²+18　　　　　　　　

(2)2x²+7xy-y²

1．选择题

　　 (1)(2005，绵阳)对x²-3x+2分解因式，结果为(　 )

　　 (A)x(x-3)+2　　　 (B)(x-1)(x-2)

　　 (C)(x-1)(x+2)　　 (D)(x+1)(x-2)

　　 (2)(2005，盐城)下列因式分解中，结果正确的是(　 )

　　 (A)x²-4=(x+2)(x-2)　　　 (B)1-(x+2)²=(x+1)(x+3)

　　 (C)2m²n-8n³=2n(m²-4n²)　 (D)x²-x+=x²(1-+)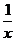

　　 (3)(2005，四川)把多项式ac-bc+a²-b²分解因式的结果是(　 )

　　 (A)(a-b)(a+b+c)　　 (B)(a-b)(a+b+c)

　　 (C)(a+b)(a-b-c)　　 (D)(a+b)(a-b+c)

　　 (4)下列因式分解中，错误的是(　 )

　　 (A)2a³-8a²+12a=2a(a²-4a+6)　 (B)x³-5x-6=(x-2)(x-3)

　　 (C)-x³+3x²-x=x(2x-1)(x-1)　 (D)x²+xy+xz+yz=(x+y)(x+z)

4．因式分解是式的变形的基本功，用处很大，必须熟练掌握，分解时要快而准．

备考例题指导

　　 例1．分解因式

　　 (1)m²(m-n)²-4(n-m)²．

　　 解：原式=m²(m-n)²-4(m-n)²

　　　　　 =(m-n)²(m²-4)

　　　　　 =(m-n)²(m+2)(m-2)

　　 (2)2a(x-y)³+2a³(y-x)．

　　 解：原式=2a(x-y)[(x-y)²-a²]

　　　　　 =2a(x-y)(x-y+a)(x-y-a)

　　 例2．分解因式

　　 (1)-2x³+3x²-x．

　　 解：原式=-x(2x²-3x+1)

　　　　　 =-x(2x-1)(x-1)

　　 (2)-xⁿ⁺⁴+xⁿ⁺¹．

　　 解：原式=-xⁿ⁺¹(x³-1)

　　　　　 =-xⁿ⁺¹(x-1)(x²+x+1)

　 　说明：首项为负要提出负号，提取公因式时，另一个因式中不要漏掉1．

　　 例3．在实数范围内分解因式

　　 (1)2x⁴-19x²+9．

　　 解：2x²　　 -1

　　　　 x²　　 -9

　　 原式=(2x²-1)(x²-9)

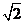　　　 　=(x+1)(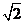x-1)(x+3)(x-3)，

　　 (2)2x²-8x+5．

　　 解：原式=2(x-x₁)(x-x₂)

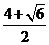　　 　　　　=2(x-)(x-)．

　　 例4．若3x²-4x+2m在实数范围内可分解因式，求m的取值范围．

　　 解：△=(-4)²-4×3×2m≥0，

　　 即m≤．

备考巩固练习

3．因式分解的一般步骤

　　 先看有没有公因式，若有立即提出；然后看看是几项式，若是二项式则用平方差、立方或立方差公式；若是三项式用完全平方公式或十字相乘法；若是四项及以上的式子用分组分解法，要注意分解到不能再分解为止，还要注意题目要求什么范围内分解．

　　 如x⁴-4=(x²+2)(x²-2)(在有理数范围内分解)

　　　　 　=(x²+2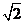)(x+)(x-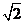)(在实数范围内分解)

　　 一般没有作说明，都只分解到有理数范围内．

2．因式分解的方法

　　 (1)提取公因式法(首先考虑的方法)、应用公式法、分组分解法、十字相乘法．

　　 (2)公式：a²-b²=_______，a²±2ab+b²=_______，a³+b³=________，a³-b³=________．

　　 (3)二次三项式ax²+bx+c在实数范围分解为：ax²+bx+c=a(x-x₁)(x-x₂)，其中x₁、x₂是方程ax²+bx+c=0的二根．

1．因式分解定义：把一个多项式化成几个_______式乘积的形式．因式分解与整式的乘法是互为________．

8. “华联”商厦进货员在苏州发现一种应季衬衫,预料能畅销市场,就用8000元购进所有衬衫,还急需2倍这种衬衫,经人介绍又在上海用176000元购进所需衬衫,只是单价比苏州贵4元,商厦按每件58元销售,销路很好,最后剩下的150件按八折销售,很快售完,问商厦这笔生意盈利多少?

7. 某商店买进一批运动衣用了1000元,每件按10元卖出.假如全部卖出这批运动衣所得的款与买进这批运动衣所用的款的差就是利润,按这样计算,这次买卖所得的利润刚好是买进11件运动衣所用的款.求这批运动衣有多少件?

6. 某农户在山上种了柚桃树88株，现进入第三年收获时，先随意采摘5株果树上的桃子，称得每株果树上的桃子产量如下(单位：千克)35、35、34、39、37。

(1)根据样本平均数估计，这年桃子的总产量是多少？

(2)若市场上的柚桃售价为每千克5元,则这年该农户卖柚桃的收入将达到多少元?

(3)已知该农户第一年卖柚桃的收入为11000元,根据以上估算,试求第二年、第三年卖柚桃收入的年平均增长率.