
题目列表(包括答案和解析)
4、下列计算正确的是 ( )
A、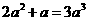 B、
B、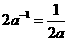 C、
C、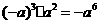 D、
D、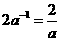
3、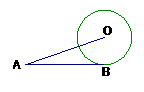 如图,AB与⊙O切于点B,AO=6㎝,AB=4㎝,则⊙O的半径为 ( )
如图,AB与⊙O切于点B,AO=6㎝,AB=4㎝,则⊙O的半径为 ( )
A、4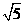 ㎝ B、2
㎝ B、2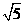 ㎝
㎝
C、2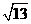 ㎝ D、
㎝ D、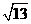 ㎝
㎝
2、计算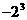 是 ( )
是 ( )
A、-8 B、8 C、-6 D、6
说明:将下列各题唯一正确的答案代号A、B、C、D填到题后的括号内。
1、在平面直角坐标系中,点P(3, -2)在 ( )
A、第一象限 B、第二象限 C、第三象限 D、第四象限
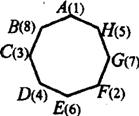
15.(1)不难验证,如图所示填法满足.s1,s2,…s8都大于或等于12.
 (2)显然,每个顶点出现在全部8组3个相邻顶点组的3个组中,所以有s1+S2+…+S8= (1+2+3+…+8)·3=108.如果每组三数之和都大于或等于13,因13·8=104,所以至多有108-104=4个组的三数之和大于13.由此我们可得如下结论:(1)相邻两组三数之和一定不相等.设前一组为(i,j,k),后一组为(j,k,l).若有i+j+k=j+k+l,则l=i,这不符合填写要求;(2)每组三数之和都小于或等于14.因若有一组三数之和大于或等于15,则至多还有另外两个组,其三数之和大于13,余下5个组三数之和等于13,必有相邻的两组相等,这和上述结论(1)不符.因此,相邻两组三数之和必然为13或14.不妨假定1填在B点上,A点所填为i,C点所填为j.(1)若S1=i+1+J=13,则.s2=1+j+l=14,S3=j+l+k=13,因J>1,这是不可能的.(2)若sl=i+1+j=14,则S2=1+j+(i-1)=13,S=j+(i-1)+2:14,s4=(i-1)+2+(j-1)=13,这时S5=14,只能是S=2+(j-1)+i,i重复出现:所以不可能有使得每组三数之和均大于或等于13的填法.
(2)显然,每个顶点出现在全部8组3个相邻顶点组的3个组中,所以有s1+S2+…+S8= (1+2+3+…+8)·3=108.如果每组三数之和都大于或等于13,因13·8=104,所以至多有108-104=4个组的三数之和大于13.由此我们可得如下结论:(1)相邻两组三数之和一定不相等.设前一组为(i,j,k),后一组为(j,k,l).若有i+j+k=j+k+l,则l=i,这不符合填写要求;(2)每组三数之和都小于或等于14.因若有一组三数之和大于或等于15,则至多还有另外两个组,其三数之和大于13,余下5个组三数之和等于13,必有相邻的两组相等,这和上述结论(1)不符.因此,相邻两组三数之和必然为13或14.不妨假定1填在B点上,A点所填为i,C点所填为j.(1)若S1=i+1+J=13,则.s2=1+j+l=14,S3=j+l+k=13,因J>1,这是不可能的.(2)若sl=i+1+j=14,则S2=1+j+(i-1)=13,S=j+(i-1)+2:14,s4=(i-1)+2+(j-1)=13,这时S5=14,只能是S=2+(j-1)+i,i重复出现:所以不可能有使得每组三数之和均大于或等于13的填法.
1.A 2.C 3.D 4.A 5.C 6.A 7.C 8.A9.2;2 10.6 11.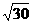 12.
12.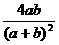

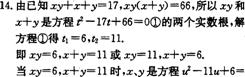

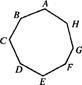
15.将数字1,2,3,4,5,6,7,8分别填写到八边形ABCDEFGH的8个顶点上,并且以S1,S2,…,S8分别表示(A,B,C),(B,C,D),…,(H,A,B)8组相邻的三个顶点上的数字之和.
(1)试给出一个填法,使得S1,S2,…,S8都大于或等于12;
(2)请证明任何填法均不可能使得S1,S2,…,S8都大于或等于13.
2006年宁波市重点中学提前招生数学试卷
14.已知x、y均为实数,且满足xy+x+y=17,x2y+xy2=66,求x4+x3y+x2y2+xy3+y4的值.
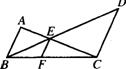
13.如图,AB∥EF∥CD,已知 AC+BD=240,BC=100,EC+ED=192,求CF.
12.已知矩形A的边长分别为a和b,如果总有另一矩形B,使得矩形B与矩形A的周长之比与面积之比都等于k,则k的最小值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com