
题目列表(包括答案和解析)
1.任何一个算法都必须有的基本结构是( ).
A 顺序结构 B 条件结构 C 循环结构 D 三个都有
20. (本题满分16分)如图,给出了一个三角形数阵,已知每一列的数成等差数列,从第3行起,每一行的数成等比数列,每一行的公比都相等.记第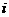 行第
行第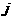 列的数为
列的数为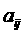 (
(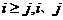 ∈N*).
∈N*).
(1)试写出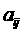 关于
关于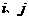 的表达式,并求
的表达式,并求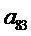 ;
;
(2)设数阵中第n行的所有数之和为An, 求An
(3)这个数阵共有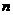 行,求数阵表中的所有数之和.
行,求数阵表中的所有数之和.
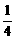
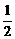 ,
,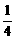
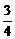 ,
,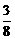 ,
,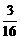
19.(本小题满分16分)定义:若数列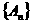 满足
满足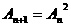 ,则称数列
,则称数列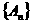 为“平方递推数列”。已知数列
为“平方递推数列”。已知数列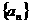 中,
中,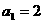 ,点
,点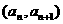 在函数
在函数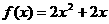 的图像上,其中
的图像上,其中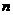 为正整数。
为正整数。
(1)证明:数列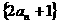 是“平方递推数列”,且数列
是“平方递推数列”,且数列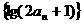 为等比数列。
为等比数列。
(2)设(1)中“平方递推数列”的前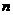 项之积为
项之积为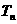 ,即
,即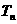
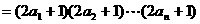 ,求数列
,求数列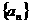 的通项及
的通项及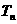 关于
关于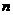 的表达式。
的表达式。
(3)记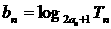 ,求数列
,求数列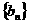 的前
的前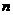 项之和
项之和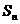 ,并求使
,并求使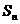
 的
的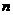 的最小值。
的最小值。
18.(本小题满分16分,第一、第二小问满分各8分)在等比数列 中,
中,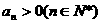 ,公比
,公比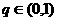 ,且
,且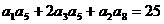 ,又
,又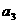 与
与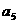 的等比中项为
的等比中项为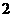 ,
,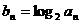 ,数列
,数列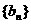 的前
的前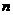 项和为
项和为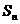 。
。
(1)求数列 的通项公式。
的通项公式。
(2)求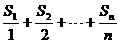 最大值?
最大值?
17.(本小题满分14分,第一、第二小问满分各7分)
已知函数
(1)写出函数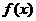 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)若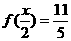 且
且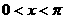 ,求
,求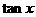 的值.
的值.
16.(本小题满分14分)
在△ABC中,角A、B、C所对的边分别是a、b、c,若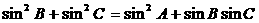 ,且
,且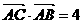 ,求△ABC的面积S.
,求△ABC的面积S.
15.(本小题14分,第一、二两小问满分各7分)
已知数列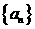 是等差数列,
是等差数列,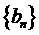 是等比数列,且
是等比数列,且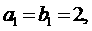
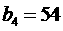 ,
, 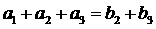 ,(I)求数列
,(I)求数列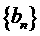 的通项公式;(II)求数列
的通项公式;(II)求数列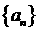 的前10项和
的前10项和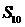 。
。
14.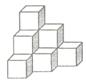 将棱长相等的正方体按右图所示的形状摆放,从上往下依次为第1层,第2层,第3 层,…,则第6层正方体的个数是
。
将棱长相等的正方体按右图所示的形状摆放,从上往下依次为第1层,第2层,第3 层,…,则第6层正方体的个数是
。
13.假设实数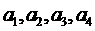 是一个等差数列,且满足
是一个等差数列,且满足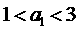 及
及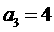 .若定义
.若定义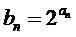 ,给出下列命题:①
,给出下列命题:①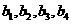 是一个等比数列;②
是一个等比数列;②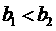 ;③
;③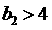 ;④
;④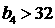 ;⑤
;⑤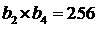 .其中正确的命题序号为
.
.其中正确的命题序号为
.
12.小明是戴南高级中学2007级高一学生,为他将来读大学的费用做好准备,他的父母计划从2008年7月1日起至2010年7月1日每月定期到银行存款m元(按复利计算),2010年8月1日全部取出,月利率按2‰计算,预计大学费用为4万元,那么m=
(计算结果精确到元。可以参考以下数据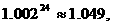
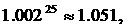
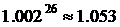 )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com