
题目列表(包括答案和解析)
4.已知函数y=x2+ax+3的定义域为[-1,1]且当x=-1时,函数有最小值;当x=1时,函数有最大值,则a满足( ).
A.0<a≤2 B.a≥2 C.a<0 D.a∈R
3.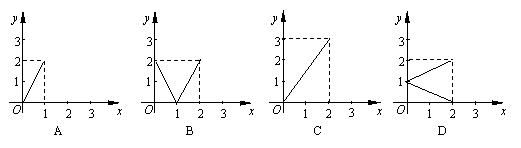 设集合M={x|0≤x≤2},集合N={y|0≤y≤2},下图给出4个图形分别表示集合M到集合N的对应,其中是从集合M到集合N的函数的是( ).
设集合M={x|0≤x≤2},集合N={y|0≤y≤2},下图给出4个图形分别表示集合M到集合N的对应,其中是从集合M到集合N的函数的是( ).
2.若全集U={1,2,3,4},集合A={1,2},则满足A∪B=U的集合B是( ).
A.1个 B.2个 C.3个 D.4个
1.已知集合A={x|≤x<}和m=π,则下列关系中正确的是( ).
A.mÍA B.mA C.{m}∈A D.{m}ÍA
22. (本题满分12分)
(1)
证:任取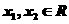 且
且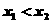 ,∴
,∴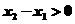 ,
,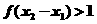
∵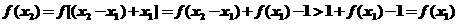
∴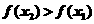
∴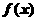 在R上为增函数
在R上为增函数
(2)∵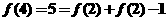
∴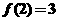
∴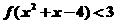 即
即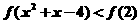
∵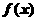 在R上为增函数
在R上为增函数
∴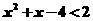
∴
(3)令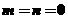
∴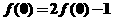
∴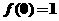
∵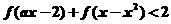 即
即 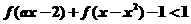
∴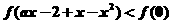
由①知 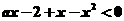 恒成立
恒成立
∴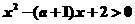 恒成立
恒成立
∴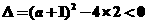
∴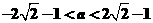
21. (本题满分12分)⑴在△ABC中,因为角A为锐角且  ,
,
所以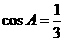
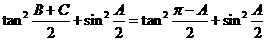
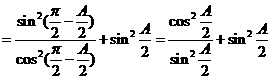
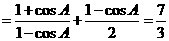
⑵由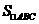
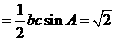 ,得
,得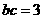 ①
①
由余弦定理,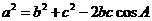 ,即
,即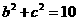 ②
②
由①②解得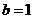 或
或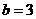
20. (本题满分12分)⑴ 当n = 1时,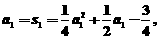
解出a1 = 3
⑵ 又4sn = an2 + 2an-3 ①
4sn-1 = 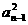 + 2an-3 (n≥2) ②
+ 2an-3 (n≥2) ②
①-② 4an = an2-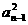 + 2an-2an-1
+ 2an-2an-1
即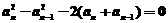
∴ 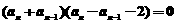
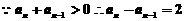 (
(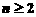 )
)
 是以3为首项,2为公差之等差数列
是以3为首项,2为公差之等差数列
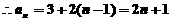
⑶ 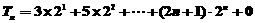 ③
③
又 ④
④
④-③ 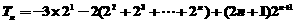
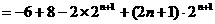
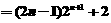
∴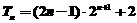
19. (本题满分12分)(1)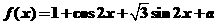
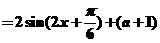
当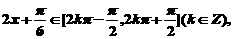
即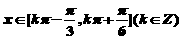 时,
时,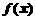 为增函数
为增函数
(2)当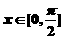 时,
时,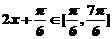
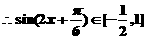 ,
,
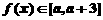
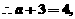
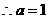
当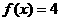 时,
时,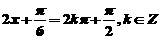
即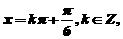
又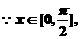

17(本题满分13分)(1)由已知有: 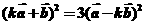
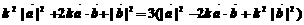
∴ 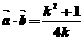
(2)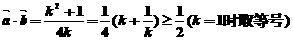
此时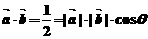
∴ 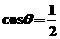 ∴
∴ 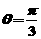
18. (本题满分13分)(1)在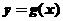 上任取一点
上任取一点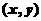 ,它关于原点对称点为
,它关于原点对称点为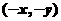 , 则
, 则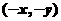 在
在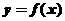 上
上
∴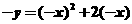 即
即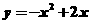
∴ 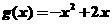
(2)不等式即: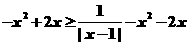
∴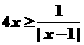 即
即 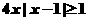
∴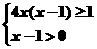 或
或 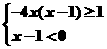
∴ 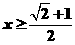 或
或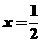
∴ 不等式解集为 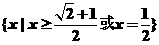
13. 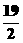 14.
14.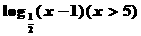 15.2
16.
15.2
16.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com