
题目列表(包括答案和解析)
21. (本小题满分15分)已知定点A(-1,0)和B(1,0),P是圆(x-3)2+(y-4)2=4上的一动点,求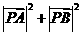 的最大值和最小值.
的最大值和最小值.
分析:因为O为AB的中点,所以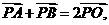 故可利用向量把问题转化为求向量
故可利用向量把问题转化为求向量 的最值。
的最值。
解:设已知圆的圆心为C,由已知可得: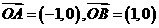 …2分
…2分

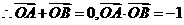 又由中点公式得
又由中点公式得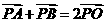 …4分
…4分
所以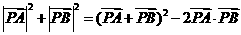
=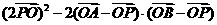
=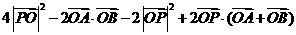
=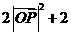 …8分
…8分
又因为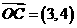 点P在圆(x-3)2+(y-4)2=4上,
点P在圆(x-3)2+(y-4)2=4上,
所以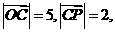 且
且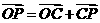 …10分
…10分
所以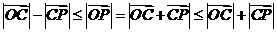 …12分
…12分
即
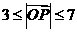 故
故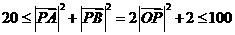 …14分
…14分
所以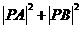 的最大值为100,最小值为20.
…15分
的最大值为100,最小值为20.
…15分
20. (本小题满分13分)已知函数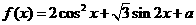 (x∈R).
(x∈R).
⑴若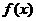 有最大值2,求实数a的值;⑵求函数
有最大值2,求实数a的值;⑵求函数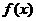 的单调递增区间.
的单调递增区间.
解:⑴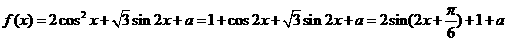 ,
,
当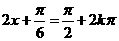 (k∈Z)时,
(k∈Z)时,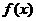 有最大值,
…3分
有最大值,
…3分
即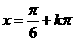 (k∈Z)时,
(k∈Z)时,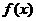 有最大值为3+a,∴3+a=2,解得
有最大值为3+a,∴3+a=2,解得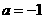 ;…6分
;…6分
⑵令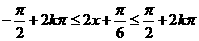 ,
…9分
,
…9分
解得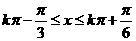 (k∈Z)
…12分
(k∈Z)
…12分
∴函数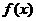 的单调递增区间
的单调递增区间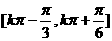 (k∈Z). …14分
(k∈Z). …14分
19. (本小题满分13分)已知α∈(0,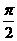 ),且cos2α=
),且cos2α=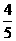 .
.
(Ⅰ)求sinα+cosα的值;
(Ⅱ)若b∈(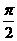 ,π),且5sin(2α+β)=sinβ,求角β的大小 .
,π),且5sin(2α+β)=sinβ,求角β的大小 .
解:(I)由cos2α=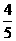 ,得1-2sin2α=
,得1-2sin2α=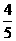 .
……2分
.
……2分
所以sin2α=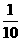 ,又α∈
,又α∈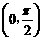 ,所以sinα=
,所以sinα=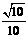 .
……3分
.
……3分
因为cos2α=1-sin2α,所以cos2α=1-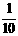 =
=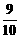 .
.
又α∈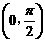 ,所以cosα=
,所以cosα=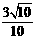 ……5分
……5分
所以sinα+cosα=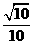 +
+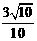 =
=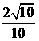 .
……6分
.
……6分
(Ⅱ)因为α∈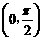 ,所以2α∈
,所以2α∈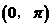 ,
,
由已知cos2α=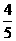 ,所以sin2α=
,所以sin2α=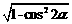 =
= 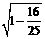 =
= 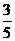 ……7分
……7分
由5sin(2α+β)=sinβ,得5(sin2αcosβ+cos2αsinβ)=sinβ. ……9分
所以5(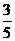 cosβ+sinβ)=sinβ,即3cosβ=-3sinβ,所以tanβ=-1. ……11分
cosβ+sinβ)=sinβ,即3cosβ=-3sinβ,所以tanβ=-1. ……11分
因为β∈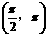 , 所以β=
, 所以β=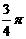 .
……13分
.
……13分
18. (本小题满分12分)已知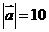 、
、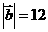 ,
,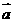 与
与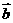 的夹角为120°,求:⑴
的夹角为120°,求:⑴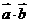 ;⑵
;⑵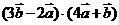 .
.
解:⑴ ;
…6分
;
…6分
⑵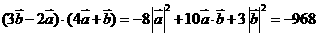 …12分
…12分
17. (本小题满分12分)设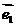 ,
,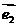 是两个相互垂直的单位向量,且
是两个相互垂直的单位向量,且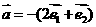 ,
,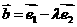 .
.
(1)若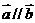 ,求
,求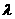 的值;
的值;
(2)若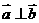 ,求
,求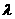 的值.
的值.
解法一:(1)由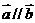 ,且
,且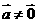 ,故存在唯一的实数
,故存在唯一的实数 ,使得
,使得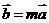 ,
,
即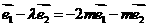
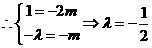 …6分
…6分
(2)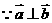 ,
,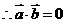 ,即
,即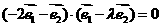
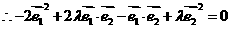 ,
,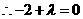 ,
,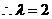 …12分
…12分
解法二:∵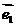 ,
,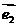 是两个相互垂直的单位向量,
是两个相互垂直的单位向量,
∴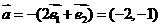 、
、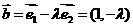 ,
…4分
,
…4分
⑴∵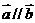 ,∴
,∴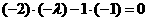 ,解得
,解得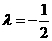 ;
…8分
;
…8分
⑵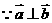 ,
,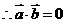 ,即
,即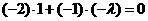 ,解得
,解得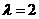 。…12分
。…12分
16. (本小题满分10分) 已知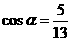 ,且角
,且角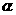 是第四象限角,求
是第四象限角,求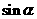 与
与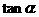 的值.
的值.
解: ∵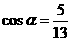 、且角
、且角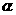 是第四象限角,
…2分
是第四象限角,
…2分
∴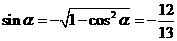 ,
…6分
,
…6分
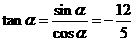 .
…10分
.
…10分
15.已知函数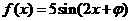 ,若对任意x∈R,都有
,若对任意x∈R,都有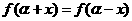 ,则
,则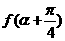 =____.
=____.
解:0。
14.设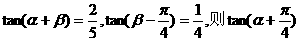 的值等于____ .
的值等于____ .
解: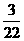 .
.
13. sin15°cos15°的值等于____ .
解:sin15°cos15°=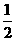 sin30°=
sin30°=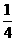 .
.
12.已知点A(1,2)、B(3,4),则向量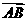 坐标为____ .
坐标为____ .
解:(2,2).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com