8．已知、是非零向量且满足，，则与的夹角是(　　 )

(A)　　　 (B)　　 (C)　　　 (D)

7．函数是　　　　　　　　　　　　　 (　 )

　　　 A．奇函数　　　　　　　　　　　　　　　　　　　　　 B．偶函数 　　　　　

　　　 C．非奇非偶函数　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．既是奇函数又是偶函数

6．函数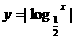的定义域为[]，值域为[0，2]

则的最小值是　　　　　　　　　　　 (　 )　　

　A．　　　 B．3　　　　　　　 C．　　　　　　　 D．2

5．平面五边形ABCDE中，向量+ ++ =(　 )

A． 　　B．　 　　　C．　 　 D．

4．对于函数y=f(x),定义域为D,任意，∈D, < 总有f<f，则称f(x)为“实验中学”函数，下列函数是“实验中学”函数的是　　　　　　　　　　　　　　 (　 )

A．　 y=－ (xÎR，x≠0 )　

B．y=tanx (xÎR ，x≠k+ ,k∈Z)　

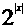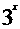C．y= (xÎR)　　　　 D．y= (xÎR)

3．函数y=sinx(x∈R)图象的对称轴方程中有一个是　 (　　 )

　 A．x=0　　　 B．x=　　　　 C．x=　　　　 D．x=2

2.二次函数 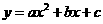中，　 ，则函数的零点

个数是(　 )

A　 0个　　　　 B　 1个　　 C　 2个　　　　 D　 无法确定

1．若函数的定义域为，则其值域为　 (　 )　　　　　　　

　　 A　　　　 B．　

C．　　 D．

21．解：(1)由f(x)=a^x+3a，得，x>3a. 又函数y=g(x)的图象与y=f^－1(x)的图象关于点(a，0)对称，设P(x，y)为y=g(x)图象上任一点，则点P关于点(a，0)的对称点(2a－x，－y)在y=f^－1(x)的图象上，∴－y=log_a(2a－x－3a)　 则有：g(x)=－f^－1(2a－x)=－log_a(－x－a)，x<－a.

　　　 (2)假设存在实数a，使得当x∈[a+2，a+3]时，不等式|f^－1(x)－g(－x)|≤1恒成立，则有

|log_a(x－3a)+log_a(x－a)|≤1，x>3a，即－1≤log_a(x²－4ax+3a²)≤1. 由3a<a+2及a>0，

　　　 解不等式①，得或.

　　　 由题设知[a+2，a+3]，

∴或 结合0<a<1，解得

　　　 对于不等式②，令h(x)=x²－4ax+3a²－，则[a+2，a+3]是不等式h(x)≤0的解集的子集的充要条件是 结合0<a<1，解得

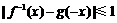　　　 综上所述，存在，使得当x∈[a+2，a+3]时，不等式恒成立.

20．解：(1)大小关系：m(x)>n(x).

　　　 (2)设P(x，y)，其中x>0. 由P在直线g(x)=x上，∴设P(t，t)，由t=2^x，得，

∴A(log₂t，t). 由log₂t=y，得B(t，log₂t). ∵|PA|=|t－log₂t|，|PB|=|t－log₂t|，∴|PA|=|PB|.

　　　 (3)F(x)=f(|x－1|)+f(|x+2|)=log₂|x－1|+log₂|x+2|=，

其中x≠1，且x≠－2.　 ∴当时，，当x=－1或0时，∴f(x)_min=1.