
题目列表(包括答案和解析)
例2.高一(1)班学生期终考试成绩表明:(1)36人数学成绩不低于80分;(2)20人物理成绩不低于80分;(3)15人的人数学、物理成绩不低于80分.问:有多少人这两科成绩至少有一科不低于80分?
分析:利用Venn图表示数学、物理不低于80分的人数的直观图,实质上是求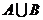 的元素的个数,从而利用方程的思想解出题中的问题.
的元素的个数,从而利用方程的思想解出题中的问题.
 解:设数学、物理不低于80分的人数的集合分别是A、B,并用二个圆分别表示,则重叠的部分表示同时不低于80分的人数的集合。则A有36个元素,B有20个元素,
解:设数学、物理不低于80分的人数的集合分别是A、B,并用二个圆分别表示,则重叠的部分表示同时不低于80分的人数的集合。则A有36个元素,B有20个元素,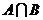 有15个元素,由
有15个元素,由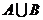 定义知,
定义知,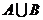 的元素有三部分:
的元素有三部分:
(1) 属于A但不属于B的元素有(36-15)个;
(2) 属于B但不属于A的元素有(20-15)个;
(3) 属于A,B的公共元素有15个;
故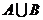 的有(36-15)+(20-15)+15=41(个元素).
的有(36-15)+(20-15)+15=41(个元素).
评:先转化为集合语言,再用Venn图的直观性是解决实际问题中交、并集有关知识的重要手段。
例3.设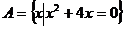 ,函数
,函数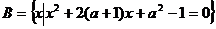 ,求使(1)
,求使(1)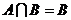 的实数a的取值范围。(2)使
的实数a的取值范围。(2)使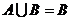 的实数a的值.
的实数a的值.
分析:交、并集有如下性质:①若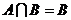 ,则
,则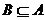 ②若
②若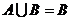 ,则
,则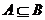 等
等
解:(1)由 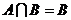 ,得
,得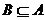 ,∵
,∵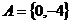 ,故:①当
,故:①当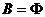 时,
时,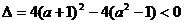 ,解得
,解得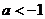 ;②当
;②当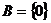 或
或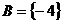 时
时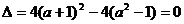 ,解得
,解得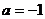 ,此时
,此时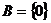 ,满足
,满足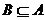 ;③当
;③当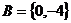 时当
时当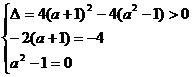 ,解得
,解得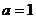
综上所述,实数a的取值范围是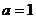 或
或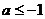
(2)由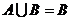 ,得
,得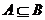 ,∵
,∵ ,故
,故 ,即
,即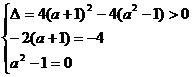 ,解得
,解得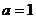
评:利用交、并集的性质,把交、并集的运算转化为集合与集合之间的子集关系的运算。
例1.已知集合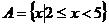 ,
,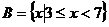 ,求
,求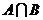 ,
,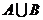
分析:利用数行结合的思想,将满足条件的集合在数轴上一一表示出来,从而求集合的交集与并集。
 解:利用数轴工具,画出集合A、B的示意图。如图:即可以得到
解:利用数轴工具,画出集合A、B的示意图。如图:即可以得到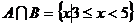 ,
,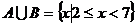
例2.(06江苏高考)设A,B,C为三个集合,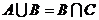 。则一定有:(A)
。则一定有:(A) 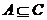 (B)
(B) 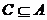 (C)
(C)
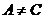 (D)
(D)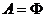
解:根据交、并集的定义与Venn图,选择A
评:这种利用数轴或Venn图等数形结合的方式,既简单又直观,是解决这类问题的基本方法。
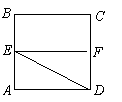
19.(本小题满分12分)
已知正方形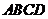 ,
,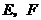 分别是边
分别是边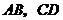 的中点,将
的中点,将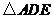 沿
沿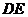 折起,如图所示,记二面角
折起,如图所示,记二面角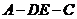 的大小为
的大小为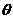 (
(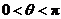 ).
).
(1)证明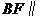 平面
平面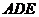 ;
;
(2)若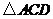 为正三角形,试判断点
为正三角形,试判断点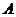 在平面
在平面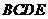 内的射影
内的射影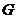 是否在直线
是否在直线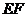 上,证明你的结论,并求角
上,证明你的结论,并求角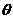 的余弦值.
的余弦值.

(19)本小题主要考查空间中的线面关系,解三角形等基础知识,考查空间想象能力和思维能力.满分12分
(Ⅰ)证明: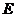 、
、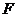 分别是正方形
分别是正方形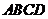 的边
的边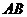 、
、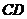 的中点.
的中点.
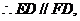 且
且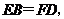
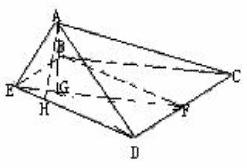
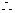 四边形
四边形 是平行四边形
是平行四边形
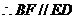
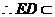 平面
平面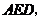 而
而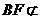 平面
平面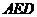
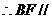 平面
平面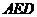
(Ⅱ)解法一:点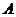 在平面
在平面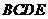 内的射影
内的射影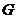 在直线
在直线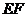 上,过点
上,过点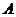 用
用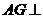 平面
平面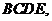 垂足为
垂足为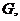 连接
连接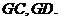
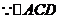 为正三角形
为正三角形
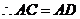
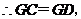
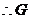 在
在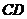 的垂直平分线上。
的垂直平分线上。
又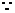
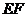 是
是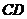 的垂直平分线
的垂直平分线
 点
点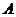 在平面
在平面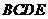 内的射影
内的射影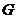 在直线
在直线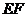 上
上
过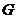 作
作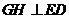 ,垂足为
,垂足为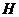 ,连接
,连接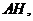 则
则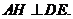
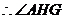 是二面角
是二面角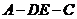 的平面角,即
的平面角,即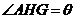
设原正方形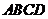 的边长为
的边长为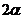 ,连接
,连接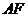 ,
,
在折后图的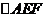 中,
中,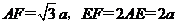
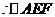 为直角三角形,
为直角三角形,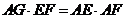
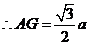
在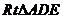 中,
中,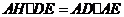
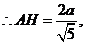
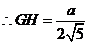
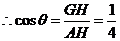
解法二:点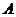 在平面
在平面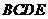 内的射影
内的射影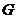 在直线
在直线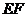 上,连结
上,连结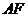 ,在平面
,在平面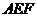 内过点
内过点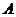 作
作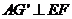 ,垂足为
,垂足为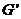
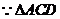 为正三角形,
为正三角形,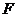 为
为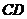 的中点,
的中点,
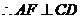
又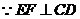
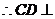 平面
平面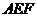
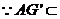 平面
平面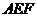
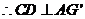
又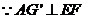 ,且
,且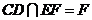 ,
,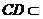 平面
平面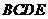 ,
,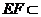 平面
平面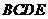 ,
,
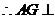 平面
平面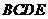 ,
,
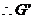 为
为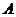 在平面
在平面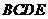 内的射影
内的射影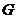 。
。
 点
点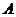 在平面
在平面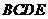 内的射影
内的射影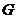 在直线
在直线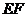 上
上
过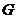 作
作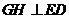 ,垂足为
,垂足为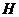 ,连结
,连结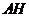 ,则
,则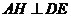 ,
,
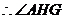 是二面角
是二面角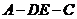 的平面角,即
的平面角,即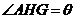
设原正方形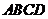 的边长为
的边长为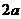 。
。
在折后图的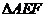 中,
中,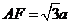 ,
,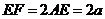
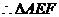 为直角三角形,
为直角三角形,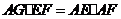 ,
,
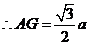 ,
,
在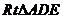 中,
中,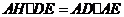 ,
,
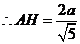 ,
,
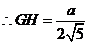
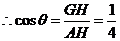
解法三:点 在平面
在平面 内的射影
内的射影 在直线
在直线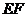 上连结
上连结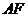 ,在平面
,在平面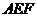 内过点
内过点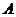 作
作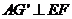 ,垂足为
,垂足为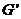
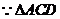 为正三角形,
为正三角形,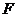 为
为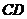 的中点
的中点
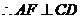
又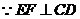
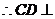 平面
平面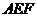 ,
,
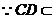 平面
平面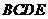 ,
,
 平面
平面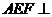 平面
平面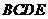
又 平面
平面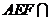 平面
平面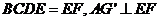 ,
,
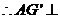 平面
平面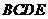 ,即
,即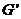 为
为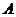 在平面
在平面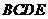 内的射影
内的射影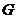 ,
,
 点
点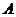 在平面
在平面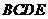 内的射影
内的射影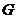 在直线
在直线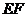 上。
上。
过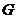 作
作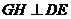 ,垂足为
,垂足为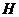 ,连结
,连结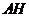 ,则
,则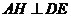
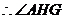 是二面角
是二面角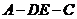 的平面角,即
的平面角,即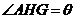
设原正方形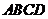 的边长为
的边长为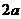
在折后图的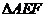 中,
中,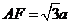
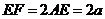 .
.
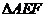 为直角三角形,
为直角三角形,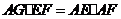 .
.
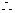
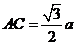 .
.
在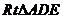 中,
中,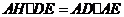 ,
,
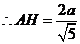 ,
,
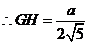 ,
,
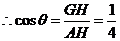 .············12分
.············12分
9.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为 ( )
A.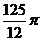 B.
B.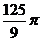 C.
C.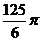 D.
D.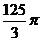
2006山东理科
(12)如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则P-DCE三棱锥的外接球的体积为
(A)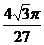 (B)
(B)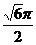 (C)
(C)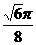 (D)
(D)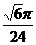
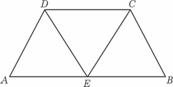
2006辽宁
12.设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E(如图).现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与AE所成角的大小等于_________.90
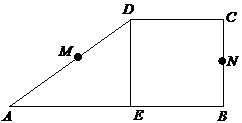
2005年高考文科数学 江西卷
江西卷
17、(本题满分12分)
如图1,已知ABCD是上、下底边长分别为2和6,高为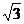 的等腰梯形,将它沿对称轴OO1折成直二面角,如图2。
的等腰梯形,将它沿对称轴OO1折成直二面角,如图2。
(Ⅰ)证明:AC⊥BO1;
(Ⅱ)求二面角O-AC-O1的大小。
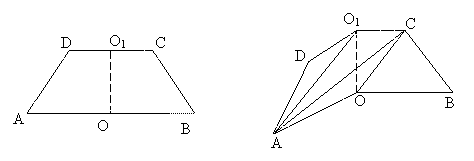
解法二(I)证明 由题设知OA⊥OO1,OB⊥OO1,
所以∠AOB是所折成的直二面角的平面角,
 即OA⊥OB. 从而AO⊥平面OBCO1,
即OA⊥OB. 从而AO⊥平面OBCO1,
OC是AC在面OBCO1内的射影.
因为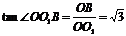
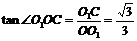 ,
,
所以∠OO1B=60°,∠O1OC=30°,从而OC⊥BO1
由三垂线定理得AC⊥BO1.
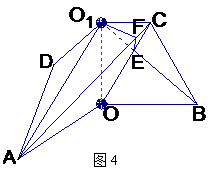
(II)解 由(I)AC⊥BO1,OC⊥BO1,知BO1⊥平面AOC.
设OC∩O1B=E,过点E作EF⊥AC于F,连结O1F(如图4),则EF是O1F在平面AOC
内的射影,由三垂线定理得O1F⊥AC.
所以∠O1FE是二面角O-AC-O1的平面角.
由题设知OA=3,OO1=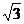 ,O1C=1,
,O1C=1,
所以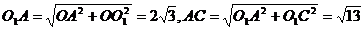 ,
,
从而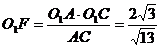 , 又O1E=OO1·sin30°=
, 又O1E=OO1·sin30°=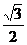 ,
,
所以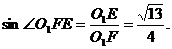 即二面角O-AC-O1的大小是
即二面角O-AC-O1的大小是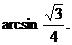
2005浙江理科
11.如图,在正三角形ABC中,D,E,F分别为各边的中点,
G,H,I,J分别为AF,AD,BE,DE的中点.将△ABC
沿DE,EF,DF折成三棱锥以后,GH与IJ所成角的度
数为 ( )
A.90° B.60°
C.45° D.0°
2004安徽春季理科
(5)等边三角形ABC的边长为4,M、N分别为AB、AC的中点,沿MN将△AMN折起,使得面AMN与面MNCB所处的二面角为300,则四棱锥A-MNCB的体积为
(A)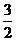 (B)
(B)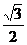 (C)
(C)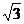 (D)3
(D)3
2005湖南高考理科
18.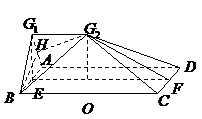 解:解法一:(I)因为平面
解:解法一:(I)因为平面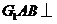 平面
平面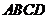 ,平面
,平面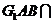 平面
平面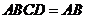 ,
,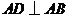 ,
,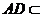 平面
平面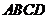 ,所以
,所以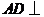 平面
平面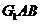 ,又
,又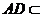 平面
平面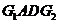 ,所以平面
,所以平面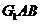
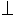 平面
平面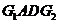 .
.
(II)过点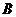 作
作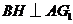 于点
于点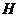 ,连结
,连结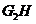 .
.
由(I)的结论可知,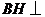 平面
平面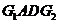 ,
,
所以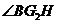 是
是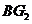 和平面
和平面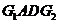 所成的角.
所成的角.
因为平面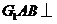 平面
平面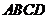 ,平面
,平面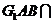 平面
平面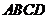
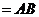 ,
,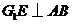 ,
,
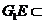 平面
平面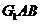 ,所以
,所以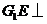 平面
平面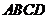 ,故
,故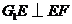 .
.
因为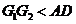 ,
,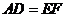 ,所以可在
,所以可在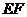 上取一点
上取一点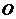 ,使
,使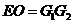 ,又因为
,又因为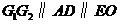 ,所以四边形
,所以四边形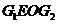 是矩形.由题设
是矩形.由题设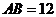 ,
,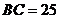 ,
,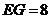 ,则
,则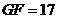 .所以
.所以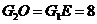 ,
,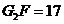 ,
,
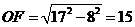 ,
,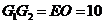 .因为
.因为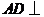 平面
平面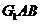 ,
,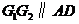 ,所以
,所以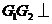 平面
平面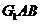 ,从而
,从而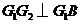 .故
.故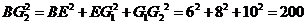 ,
,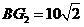 .
.
又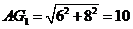 ,由
,由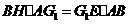 得
得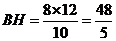 .
.
故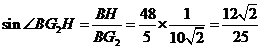 .即直线
.即直线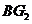 与平面
与平面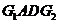 所成的角是
所成的角是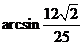 .
.
解法二:(I)因为平面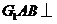 平面
平面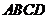 ,平面
,平面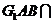 平面
平面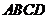
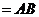 ,
,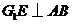 ,
,
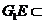 平面
平面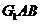 ,所以
,所以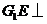 平面
平面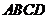 ,从而
,从而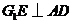 .又
.又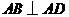 ,所以
,所以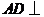 平面
平面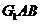 .因为
.因为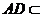 平面
平面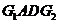 ,所以平面
,所以平面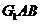
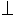 平面
平面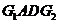 .
.
 (II)由(I)可知,
(II)由(I)可知,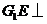 平面
平面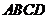 .故可以
.故可以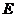 为原点,分别以直线
为原点,分别以直线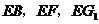 为
为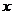 轴、
轴、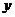 轴、
轴、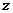 轴建立空间直角坐标系(如图),
轴建立空间直角坐标系(如图),
由题设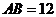 ,
,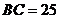 ,
,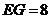 ,则
,则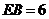 ,
,
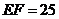 ,
,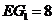 ,相关各点的坐标分别是
,相关各点的坐标分别是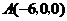 ,
,
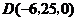 ,
,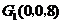 ,
,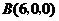 .
.
所以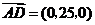 ,
,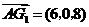 .
.
设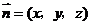 是平面
是平面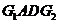 的一个法向量,
的一个法向量,
由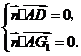 得
得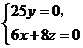 故可取
故可取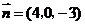 .过点
.过点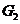 作
作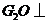 平面
平面 于点
于点 ,因为
,因为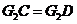 ,所以
,所以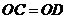 ,于是点
,于是点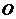 在
在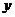 轴上.因为
轴上.因为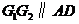 ,所以
,所以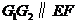 ,
,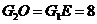 .
.
设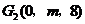 (
(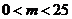 ),由
),由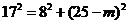 ,解得
,解得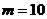 ,
,
所以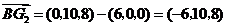 .设
.设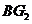 和平面
和平面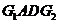 所成的角是
所成的角是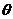 ,则
,则
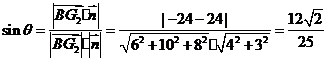 .故直线
.故直线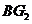 与平面
与平面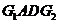 所成的角是
所成的角是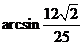 .
.
18.(2007高考湖南卷)
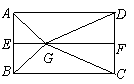
如图2,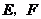 分别是矩形
分别是矩形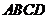 的边
的边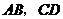 的中点,
的中点,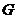 是
是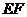 上的一点,将
上的一点,将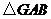 ,
,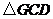 分别沿
分别沿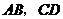 翻折成
翻折成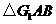 ,
,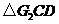 ,并连结
,并连结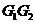 ,使得平面
,使得平面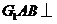 平面
平面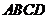 ,
,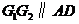 ,且
,且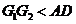 .连结
.连结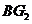 ,如图3.
,如图3.
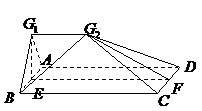
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com