20．(本小题满分12分)已知函数f(x)＝sinωx·cosωx＋cos²ωx－(ω>0)的图象上两相邻对称轴间的距离为.

(1)求f(x)的单调递减区间；

(2)将函数f(x)的图象向右平移个单位，再将所得图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，得到函数y＝g(x)的图象，求g(x)在区间[0，]上的最大值和最小值．

解：(1)f(x)＝sinωx·cosωx＋cos²ωx－＝sin2ωx＋－＝sin(2ωx＋)，

由题意知f(x)的最小正周期T＝，T＝＝＝，ω＝2，所以f(x)＝sin(4x＋)．

由2kπ＋≤4x＋≤2kπ＋(k∈Z)，得＋≤x≤＋(k∈Z)，

所以函数f(x)的单调递减区间为[＋，＋](k∈Z)．

(2)将f(x)的图象向右平移个单位后，得到y＝sin[4(x－)＋]＝sin(4x－)的图象，再将所得图象上所有点的横坐标伸长到原来的2倍，纵坐标不变，得到y＝sin(2x－)的图象．所以g(x)＝sin(2x－)．

因为0≤x≤，所以－≤2x－≤，－≤sin(2x－)≤1，

当2x－＝－，即x＝0时，g(x)_min＝－；

当2x－＝，即x＝时，g(x)_max＝1.

19．(本小题满分12分)在△ABC中，角A、B、C所对的边分别为a、b、c，已知(2a＋b)cosC＋ccosB＝0.

(1)求角C的大小；

(2)若c＝4，求使△ABC面积取得最大值时的a，b的值．

解：(1)由已知及由正弦定理得(2sinA＋sinB)cosC＋sinCcosB＝0，所以2sinAcosC＋(sinBcosC＋sinCcosB)＝0，

所以sin(B＋C)＋2sinAcosC＝0，

即sinA＋2sinAcosC＝0.

因为0<A<π，sinA>0，所以cosC＝－，所以C＝.

(2)因为△ABC的面积为S＝absinC＝ab，若使得S取得最大值，只需要ab取得最大值．

由余弦定理可得，c²＝a²＋b²－2abcosC，

即16＝a²＋b²＋ab≥3ab，故ab≤，当且仅当a＝b时取等号．

故使得△ABC面积取得最大值时a、b的取值为a＝b＝.

18．(本小题满分12分)已知函数f(x)＝sinxcosx＋sin²x－，将函数f(x)的图象向左平移个单位长度后得函数g(x)的图象，设△ABC的三个角A，B，C的对边分别为a，b，c；

(1)若f(C)＝0，c＝6,2sinA＝sinB，求a，b的值．

(2)若g(B)＝0且m＝(cosA，cosB)，n＝(1，sinA－cosAtanB)，求m·n的取值范围．

解：(1)f(x)＝sinxcosx＋sin²x－＝sin2x＋(1－cos2x)－＝sin2x－cos2x－1＝sin(2x－)－1.

f(C)＝sin(2C－)－1＝0，∴sin(2C－)＝1，∴C＝.

∵2sinA＝sinB，由正弦定理可得b＝2a　①

由余弦定理知：a²＋b²－2abcos＝36，即a²＋b²－ab＝36　②

由①②解得：a＝2，b＝4.

(2)由题意知g(x)＝sin(2x＋)－1，

∴g(B)＝sin(2B＋)－1＝0，∴sin(2B＋)＝1，∴B＝，

于是m·n＝cosA＋(sinA－cosA)＝cosA＋sinA＝sin(A＋)，

∵B＝，∴A∈(0，)，得A＋∈(，π)．

∴sin(A＋)∈(0,1]，即m·n∈(0,1]．

三、解答题

17．(本小题满分10分)[2014·河北高三质检]已知在△ABC中，内角A，B，C所对的边分别为a，b，c，且acosC＋c＝b.

(1)求角A；

(2)若a＝1，且c－2b＝1，求角B.

解：(1)由acosC＋c＝b，得sinAcosC＋sinC＝sinB，

∵sinB＝sin(A＋C)＝sinAcosC＋cosAsinC，

∴sinC＝cosAsinC，又sinC≠0，∴cosA＝，A＝.

(2)由c－2b＝1，得c－2b＝a，即sinC－2sinB＝sinA.

又A＝，∴C＝π－B，

∴sin(π－B)－2sinB＝，

整理得cos(B＋)＝.

∵0<B<π，∴<B＋<π.

∴B＋＝，即B＝.

16．已知3a＋4b＋5c＝0，且|a|＝|b|＝|c|＝1，则a·(b＋c)＝________.

解析：依题意得|3a|＝3，|4b|＝4，|5c|＝5，又3a＋4b＋5c＝0，所以向量3a、4b、5c首尾相接构成一个直角三角形，因此有a·b＝0，a·(b＋c)＝a·b＋a·c＝a·c＝|a|·|c|cosθ＝cosθ＝－(其中θ为向量a与c的夹角)．

答案：－

15．[2013·海淀区期末练习]函数f(x)＝Asin(2x＋φ)(A>0，φ∈R)的部分图象如图所示，那么f(0)＝________.

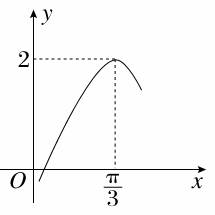
解析：由图可知，A＝2，f()＝2，

∴2sin(＋φ)＝2，sin(＋φ)＝1，

∴＋φ＝＋2kπ(k∈Z)，φ＝－＋2kπ(k∈Z)，

∴f(0)＝2sinφ＝2sin(－＋2kπ)＝2×(－)＝－1.

答案：－1

14．已知向量a＝(－，)，＝a－b，＝a＋b，若△OAB是以O为直角顶点的等腰直角三角形，则△OAB的面积为________．

解析：由题意得，|a|＝1，又△OAB是以O为直角顶点的等腰直角三角形，所以⊥，||＝||.由⊥得(a－b)·(a＋b)＝|a|²－|b|²＝0，所以|a|＝|b|，由||＝||得|a－b|＝|a＋b|，所以a·b＝0.所以|a＋b|²＝|a|²＋|b|²＝2，所以||＝||＝，故S_△OAB＝××＝1.

答案：1

二、填空题

13．已知向量a＝(8，)，b＝(x,1)，其中x>0，若(a－2b)∥(2a＋b)，则x＝________.

解析：a－2b＝(8－2x，－2)，2a＋b＝(16＋x，x＋1)，由题意得(8－2x)(x＋1)＝(－2)(16＋x)，整理得x²＝16，又∵x>0，∴x＝4.

答案：4

12．设△ABC的内角A，B，C所对的边分别为a，b，c，若(acosB＋bcosA)＝2csinC，a＋b＝4(a，b在变化)，且△ABC的面积最大值为，则此时△ABC的形状是(　)

A．锐角三角形　 　　　　　　　　　　　　 B．直角三角形

C．等腰三角形　 　　　　　　　　　　　　 D．正三角形

解析：由正弦定理得(sinAcosB＋cosAsinB)＝2sin²C，即sin(A＋B)＝sinC＝2sin²C，即sinC＝，C＝60°或120°，△ABC的面积S＝absinC＝ab≤()²＝，当且仅当a＝b时等号成立，此时a＝b＝2，选择C.

答案：C

11．若x∈[0，]，sin(x－)＝，则sin(2x＋)的值为(　)

A.　 　　　　　　　　　　　　　　　　　　　　　 B.

C.　 　　　　　　　　　　　　　　　　　　　　　 D.

解析：由sin(x－)＝得，sinxcos－cosxsin＝，sinx－cosx＝，两边平方得sin²x＋－sin2x＝，∴·＋－sin2x＝，即sin2x·＋cos2x·＝，∴sin(2x＋)＝.

答案：D