26. China is famous _________ the Great Wall and also ________ one of the largest countries with the largest population.

A. as, for　　　　　　　　 　 B. for, for　　　　 　　C. as, as　　　　　　 　 　D. for, as　

25. —What ________　 when the gang broke in?

— I ________　 the TV and was going to bed.

A．were you doing; was turning off 　　　B．did you do; has turned off

C．had you done; was turning off 　　　　D．were you doing; had turned off

24. Both my patents are ________ now. They are both ________teachers.

A. retiring; retired　　 　B. retired; retired C. retired; retiring　　　　 D. retiring; retiring

23. He made up his mind to _________ a new record in the 100-meter race.

　 　A. put down　　 B. set down　　　 C. put up　　　　　　　 D. set up

22. She ______ Japanese when she was in Japan. Now she can speak it freely. A. picked out　　　　 　　 B. made out　　　　　　C. made up　　　　　 D. picked up

第二部分 英语知识运用

第一节 单项填空(共15小题；每小题1分, 满分15分)

　　 从A、B、C、D四个选项中, 选出可以填入空白处的最佳选项, 并在答题卡上将该项涂黑。

21. 　______, they were not afraid to face the flood.

　 　A. Although surprised B. Because surprised C. If surprising　 　　 D.As long as surprising

22．(本小题满分12分)设角A，B，C是△ABC的三个内角，已知向量m＝(sinA＋sinC，sinB－sinA)，n＝(sinA－sinC，sinB)，且m⊥n.

(1)求角C的大小；

(2)若向量s＝(0，－1)，t＝(cosA,2cos²)，求|s＋t|的取值范围．

解：(1)由题意得m·n＝(sin²A－sin²C)＋(sin²B－sinAsinB)＝0，

即sin²C＝sin²A＋sin²B－sinAsinB，设a，b，c为内角A，B，C所对的边长，由正弦定理得c²＝a²＋b²－ab，

再由余弦定理得cosC＝＝，∵0<C<π，

∴C＝.

(2)∵s＋t＝(cosA,2cos²－1)＝(cosA，cosB)，

∴|s＋t|²＝cos²A＋cos²B

＝cos²A＋cos²(－A)

＝＋

＝cos2A－sin2A＋1

＝－sin(2A－)＋1，

∵0<A<，∴－<2A－<，

∴－<sin(2A－)≤1，

∴≤|s＋t|²<，∴≤|s＋t|<.

21．(本小题满分12分)[2014·长沙一模]风景秀美的凤凰湖畔有四棵高大的银杏树，记作A、B、P、Q，欲测量P、Q两棵树和A、P两棵树之间的距离，但湖岸部分地方围有铁丝网不能靠近，现可测得A、B两点间的距离为100 m，如图，同时也能测量出∠PAB＝75°，∠QAB＝45°，∠PBA＝60°，∠QBA＝90°，则P、Q两棵树和A、P两棵树之间的距离各为多少？

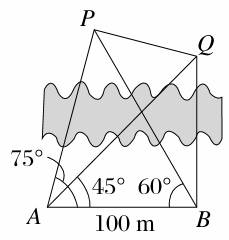
解：在△PAB中，∠APB＝180°－(75°＋60°)＝45°，

由正弦定理得＝，解得AP＝50.

在△QAB中，∠ABQ＝90°，∴AQ＝100.

又∠PAQ＝75°－45°＝30°，

由余弦定理得PQ²＝AP²＋AQ²－2AP·AQ·cos∠PAQ＝(50)²＋(100)²－2×50×100×cos30°＝5000，

∴PQ＝＝50.

∴P、Q两棵树之间的距离为50 m，A、P两棵树之间的距离为50 m.