
22(本题满分16分)本题共3个小题,第1小题满分3分,第2小题满分5分,第3小题满分8分.
在平面直角坐标系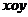 中,对于直线
中,对于直线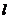 :
: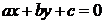 和点
和点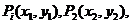 记
记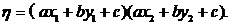 若
若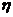 <0,则称点
<0,则称点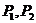 被直线
被直线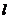 分隔。若曲线C与直线
分隔。若曲线C与直线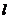 没有公共点,且曲线C上存在点
没有公共点,且曲线C上存在点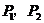 被直线
被直线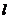 分隔,则称直线
分隔,则称直线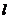 为曲线C的一条分隔线.
为曲线C的一条分隔线.
⑴ 求证:点 被直线
被直线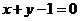 分隔;
分隔;
⑵若直线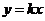 是曲线
是曲线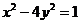 的分隔线,求实数
的分隔线,求实数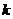 的取值范围;
的取值范围;
⑶动点M到点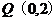 的距离与到
的距离与到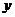 轴的距离之积为1,设点M的轨迹为E,求证:通过原点的直线中,有且仅有一条直线是E的分割线.
轴的距离之积为1,设点M的轨迹为E,求证:通过原点的直线中,有且仅有一条直线是E的分割线.
21.(本题满分14分)本题共有2个小题,第1小题满分6分,第2小题满分8分.
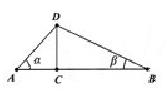
如图,某公司要在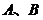 两地连线上的定点
两地连线上的定点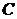 处建造广告牌
处建造广告牌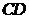 ,其中
,其中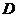 为顶端,
为顶端,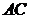 长35米,
长35米,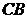 长80米,设
长80米,设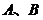 在同一水平面上,从
在同一水平面上,从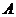 和
和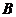 看
看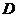 的仰角分别为
的仰角分别为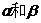 .
.
(1)设计中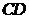 是铅垂方向,若要求zxxk
是铅垂方向,若要求zxxk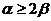 ,问
,问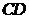 的长至多为多少(结果精确到0.01米)?
的长至多为多少(结果精确到0.01米)?
(2)施工完成后.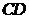 与铅垂方向有偏差,现在实测得
与铅垂方向有偏差,现在实测得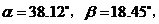 求
求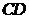 的长(结果精确到0.01米)?
的长(结果精确到0.01米)?
20.(本题满分14分)本题有2个小题,第一小题满分6分,第二小题满分1分。
设常数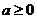 ,函数
,函数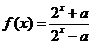
(1)若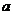 =4,求函数
=4,求函数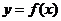 的反函数
的反函数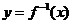 ;
;
(2)根据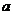 的不同取值,讨论函数
的不同取值,讨论函数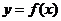 的奇偶性,并说明理由.
的奇偶性,并说明理由.
三.解答题
19、(本题满分12分)
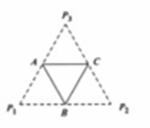
底面边长为2的正三棱锥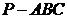 ,其表面展开图是三角形
,其表面展开图是三角形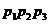 ,如图,求△
,如图,求△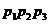 的各边长及此三棱锥的体积
的各边长及此三棱锥的体积 .
.
 zxxk
zxxk
三、解答题
(15)(本小题满分13分)
已知函数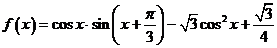 ,
,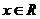 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在闭区间
在闭区间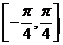 上的最大值和最小值.
上的最大值和最小值.
(16)(本小题满分13分)
某大学志愿者协会有6名男同学,4名女同学. 在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院. 现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
(Ⅰ)求选出的3名同学是来自互不相同学院的概率;
(Ⅱ)设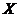 为选出的3名同学中女同学的人数,求随机变量
为选出的3名同学中女同学的人数,求随机变量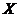 的分布列和数学期望.
的分布列和数学期望.
(17)(本小题满分13分)
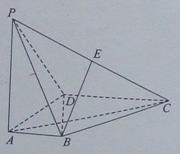 如图,在四棱锥
如图,在四棱锥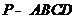 中,
中,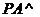 底面
底面 ,
,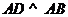 ,
,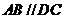 ,
,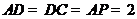 ,
,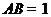 ,点
,点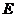 为棱
为棱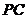 的中点.
的中点.
(Ⅰ)证明
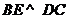 ;
;
(Ⅱ)求直线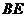 与平面
与平面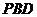 所成角的正弦值;
所成角的正弦值;
(Ⅲ)若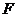 为棱
为棱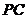 上一点,满足
上一点,满足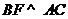 ,
,
求二面角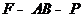 的余弦值.
的余弦值.
(18)(本小题满分13分)
设椭圆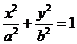 (
(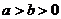 )的左、右焦点为
)的左、右焦点为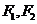 ,右顶点为
,右顶点为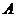 ,上顶点为
,上顶点为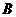 .已知
.已知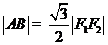 .
.
(Ⅰ)求椭圆的离心率;
(Ⅱ)设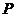 为椭圆上异于其顶点的一点,以线段
为椭圆上异于其顶点的一点,以线段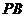 为直径的圆经过点
为直径的圆经过点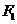 ,经过原点的直线
,经过原点的直线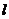 与该圆相切. 求直线的斜率.
与该圆相切. 求直线的斜率.
(19)(本小题满分14分)
已知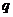 和
和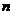 均为给定的大于1的自然数.设集合
均为给定的大于1的自然数.设集合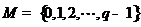 ,集合
,集合 .
.
(Ⅰ)当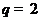 ,
,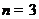 时,用列举法表示集合
时,用列举法表示集合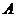 ;
;
(Ⅱ)设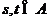 ,
,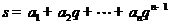 ,
,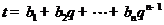 ,其中
,其中
(20)(本小题满分14分)
已知函数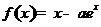
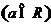 ,
,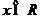 .已知函数
.已知函数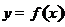 有两个零点
有两个零点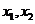 ,且
,且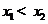 .
.
(Ⅰ)求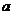 的取值范围;
的取值范围;
(Ⅱ)证明 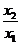 随着
随着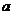 的减小而增大;
的减小而增大;
(Ⅲ)证明 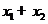 随着
随着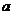 的减小而增大.
的减小而增大.
二、填空题
 (9)某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取_______名学生.
(9)某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方法,从该校四个年级的本科生中抽取一个容量为300的样本进行调查.已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取_______名学生.
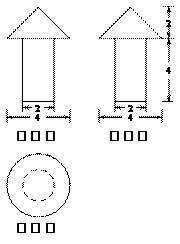
(10)已知一个几何体的三视图如图所示(单位:m),则该几何体的体积为_______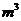 .
.
(11)设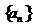 是首项为
是首项为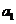 ,公差为-1的等差数列,
,公差为-1的等差数列,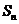 为其前
为其前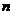 项和.若
项和.若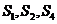 成等比数列,则
成等比数列,则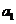 的值为__________.
的值为__________.
(12)在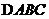 中,内角
中,内角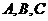 所对的边分别是
所对的边分别是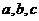 .已知
.已知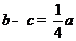 ,
,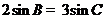 ,则
,则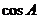 的值为_______.
的值为_______.
(13)在以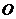 为极点的极坐标系中,圆
为极点的极坐标系中,圆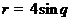 和直线
和直线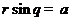 相交于
相交于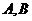 两点.若
两点.若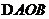 是等边三角形,则
是等边三角形,则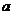 的值为___________.
的值为___________.
(14)已知函数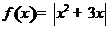 ,
,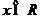 .若方程
.若方程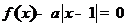 恰有4个互异的实数根,则实数
恰有4个互异的实数根,则实数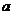 的取值范围为__________.
的取值范围为__________.
21.(本小题满分14分) 设函数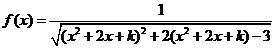 ,其中
,其中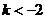 ,
,
(1)求函数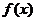 的定义域D(用区间表示);
的定义域D(用区间表示);
(2)讨论函数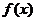 在D上的单调性;
在D上的单调性;
(3)若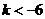 ,求D上满足条件
,求D上满足条件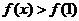 的
的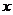 的集合(用区间表示)。
的集合(用区间表示)。
2014年普通高等学校招生全国统一考试(广东卷)
20.(本小题满分14分)已知椭圆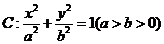 的一个焦点为
的一个焦点为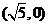 ,离心率为
,离心率为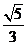 ,
,
(1)求椭圆C的标准方程;
(2)若动点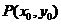 为椭圆外一点,且点P到椭圆C的两条切线相互垂直,求点P的轨迹方程。
为椭圆外一点,且点P到椭圆C的两条切线相互垂直,求点P的轨迹方程。
19.(本小题满分14分)设数列 的前
的前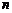 和为
和为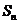 ,满足
,满足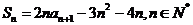 ,且
,且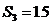 ,
,
(1)求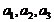 的值;
的值;
(2)求数列 的通项公式。
的通项公式。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com