
6.下列叙述中正确的是( )
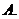 若
若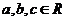 ,则
,则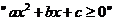 的充分条件是
的充分条件是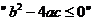
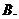 若
若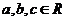 ,则
,则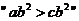 的充要条件是
的充要条件是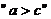
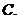 命题“对任意
命题“对任意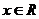 ,有
,有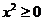 ”的否定是“存在
”的否定是“存在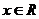 ,有
,有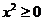 ”
”
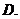
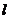 是一条直线,
是一条直线,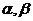 是两个不同的平面,若
是两个不同的平面,若 ,则
,则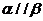
5.在在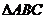 中,内角A,B,C所对应的边分别为
中,内角A,B,C所对应的边分别为 ,若
,若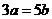 ,则
,则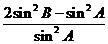 的值为( )
的值为( )
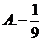
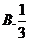
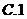
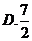
4. 已知函数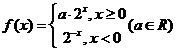 ,若
,若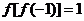 ,则
,则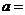 ( )
( )
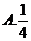
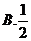
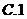
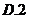
3.掷两颗均匀的骰子,则点数之和为5的概率等于( )
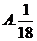
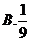
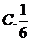
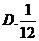
2.设全集为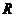 ,集合
,集合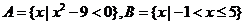 ,则
,则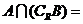 ( )
( )
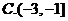
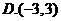
一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数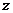 满足
满足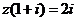 (
(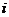 为虚数单位),则
为虚数单位),则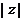 =( )
=( )
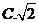
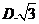
22.(1)当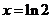 时,
时,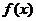 有极小值
有极小值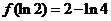 ,
,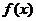 无极大值.
无极大值.
(2)见解析.(3)见解析.
解法一:
(1)由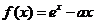 ,得
,得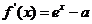 .
.
又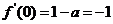 ,得
,得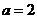 .
.
所以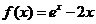 ,
,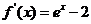 .
.
令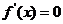 ,得
,得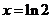 .
.
当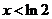 时,
时,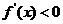 ,
,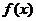 单调递减;
单调递减;
当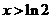 时,
时,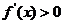 ,
,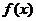 单调递增.
单调递增.
所以当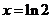 时,
时,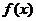 有极小值,
有极小值,
且极小值为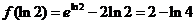 ,
,
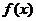 无极大值.
无极大值.
(2)令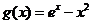 ,则
,则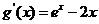 .
.
由(1)得, ,即
,即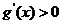 .
.
所以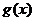 在R上单调递增,又
在R上单调递增,又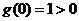 ,
,
所以当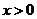 时,
时,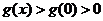 ,即
,即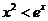 .
.
(3)对任意给定的正数c,取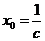 ,
,
由(2)知,当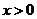 时,
时,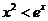 .
.
所以当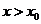 时,
时,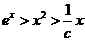 ,即
,即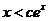 .
.
因此,对任意给定的正数c,总存在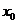 ,当
,当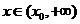 时,恒有
时,恒有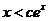 .
.
解法二:(1)同解法一.
(2)同解法一.
(3)令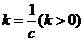 ,要使不等式
,要使不等式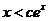 成立,只要
成立,只要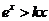 成立.
成立.
而要使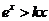 成立,则只需
成立,则只需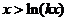 ,即
,即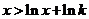 成立.
成立.
①若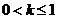 ,则
,则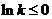 ,易知当
,易知当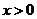 时,
时,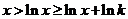 成立.
成立.
即对任意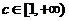 ,取
,取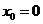 ,当
,当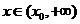 时,恒有
时,恒有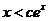 .
.
②若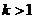 ,令
,令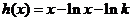 ,则
,则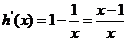 ,
,
所以当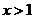 时,
时,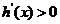 ,
,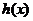 在
在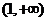 内单调递增.
内单调递增.
取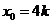 ,
,
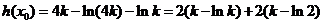 ,
,
易知 ,
,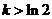 ,所以
,所以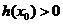 .
.
因此对任意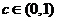 ,取
,取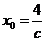 ,当
,当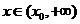 时,恒有
时,恒有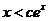 .
.
综上,对任意给定的正数c,总存在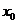 ,当
,当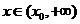 时,恒有
时,恒有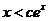 .
.
解法三:(1)同解法一.
(2)同解法一.
(3)①若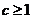 ,取
,取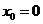 ,
,
由(2)的证明过程知,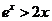 ,
,
所以当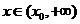 时,有
时,有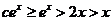 ,即
,即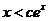 .
.
②若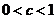 ,
,
令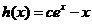 ,则
,则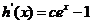 ,
,
令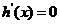 得
得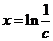 .
.
当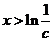 时,
时,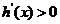 ,
,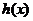 单调递增.
单调递增.
取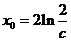 ,
,
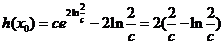 ,
,
易知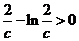 ,又
,又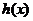 在
在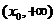 内单调递增,
内单调递增,
所以当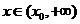 时,恒有
时,恒有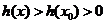 ,即
,即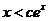 .
.
综上,对任意给定的正数c,总存在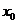 ,当
,当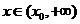 时,恒有
时,恒有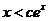 .
.
注:对c的分类可有不同的方式,只要解法正确,均相应给分。
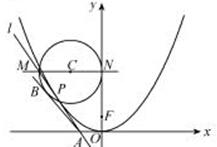
21.(1)设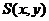 为曲线
为曲线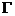 上任意一点,
上任意一点,
依题意,点S到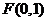 的距离与它到直线
的距离与它到直线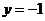 的距离相等,
的距离相等,
所以曲线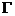 是以点
是以点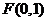 为焦点,直线
为焦点,直线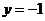 为准线的抛物线,
为准线的抛物线,
所以曲线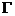 的方程为
的方程为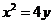 .
.
(2)当点P在曲线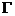 上运动时,线段AB的长度不变,证明如下:
上运动时,线段AB的长度不变,证明如下:
由(1)知抛物线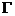 的方程为
的方程为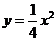 ,
,
设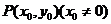 ,则
,则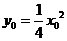 ,
,
由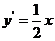 ,得切线
,得切线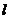 的斜率
的斜率
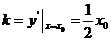 ,
,
所以切线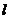 的方程为
的方程为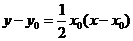 ,即
,即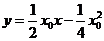 .
.
由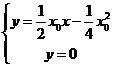 ,得
,得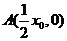 .
.
由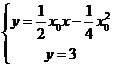 ,得
,得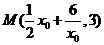 .
.
又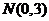 ,所以圆心
,所以圆心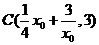 ,
,
半径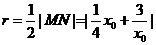 ,
,
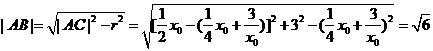 .
.
所以点P在曲线 上运动时,线段AB的长度不变.
上运动时,线段AB的长度不变.
解法二:
(1)设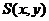 为曲线
为曲线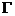 上任意一点,
上任意一点,
则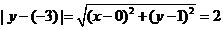 ,
,
依题意,点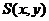 只能在直线
只能在直线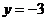 的上方,所以
的上方,所以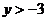 ,
,
所以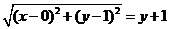 ,
,
化简得,曲线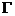 的方程为
的方程为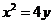 .
.
(2)同解法一.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com