
8、定义在R上的函数f(x)对任意两个不相等的实数a,b,总有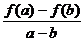 >0成立,则一定有
>0成立,则一定有
( )
A.函数f(x)是奇函数 B.函数f(x) 是偶函数
是偶函数
C.f(x)在R上是增函数 D.f(x)在R上是减函数
7、对于函数f(x),x∈[a,b]及g(x),x∈[a,b],若对 任意的x∈[a,b],总有
任意的x∈[a,b],总有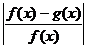 ≤
≤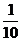 ,我们称f(x)可被g(x)替代,那么下列给出的函数中能替代 f(x)=
,我们称f(x)可被g(x)替代,那么下列给出的函数中能替代 f(x)=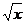 ,x∈[4,16]的是: ( )
,x∈[4,16]的是: ( )
A.g(x)=x+6,x∈[4,16] B.g(x)=x2+6,x∈[4,16]
 C.g(x)=(x+6),x∈[4,16]
D.g(x)=2x+6,x∈[4,16]
C.g(x)=(x+6),x∈[4,16]
D.g(x)=2x+6,x∈[4,16]
6、人骑车沿直线匀速旅行,先前进了a千米,休息了一段时间,又沿原路返回b千米(b<
 a,再前进c千米,则此人离起点的距离s与时间t的关系示意图是图中的 ( )
a,再前进c千米,则此人离起点的距离s与时间t的关系示意图是图中的 ( )
4、已知f(x)=(x-a)(x-b)-2,并且α、β是方程f(x)=0的两根,则实数a、b、 α、β的大小关系可能是: ( )
A.α<a<b<β B.a<α<β<b
C.α<a<b<β D.α<a<β<b
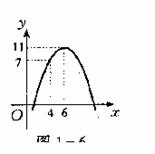 5、某汽车运输公司,购买了一批豪华大客车投入营运,据市
5、某汽车运输公司,购买了一批豪华大客车投入营运,据市 场分析每辆
客车营运
的总利润y(单位:10万元)与营运年数x(x∈N)为
场分析每辆
客车营运
的总利润y(单位:10万元)与营运年数x(x∈N)为
二次函数关 系(如图),则每辆客车营运多少年,其营
运的年平均利润最大?( )
A.3 B.4
C. 5 D.6
3、拟定从甲地到乙地通话m分钟的电话费由f(m)=1.06(0.50×[m]+1)给出,其中m >0,[m]是大于或等于m的最小整数(如[3]=3,[3.7]=4, [3.1]=4),则从甲 地到乙地通话时间为5.5分钟的话费为: ( )
A.3.71 B.3.97
C.4.24  D.4.77
D.4.77
2、若二次函数f(x)=4x 2-2(p-2)x-2p2-p+1在区间[-1,1]内至少存在一点C(c,0),使f(c)>0,则实数p的取值
2-2(p-2)x-2p2-p+1在区间[-1,1]内至少存在一点C(c,0),使f(c)>0,则实数p的取值 范围 ( )
范围 ( )
A.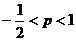 B.
B.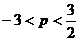
C.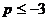 D.
D.
一、选择题:
1、在区间[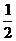 ,2]上,函数f(x)=x2+px+q与g(x)=2x+
,2]上,函数f(x)=x2+px+q与g(x)=2x+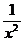 在同一点取得相同 的最
小值,那么f(x)在[
在同一点取得相同 的最
小值,那么f(x)在[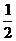 ,2]上的最大值是 ( )
,2]上的最大值是 ( )
A.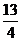 B.4
B.4
C.8 D.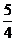
7.设函数 的定义域为
的定义域为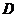 ,值域为
,值域为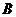 ,如果存在函数
,如果存在函数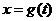 ,使得函数
,使得函数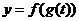 的值域仍然是
的值域仍然是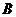 ,那么,称
,那么,称 函数
函数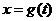 是函数
是函数 的一个等值域变换,
的一个等值域变换,
(1)判断下列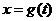 是不是
是不是 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由;
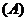
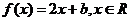 ,
, ;
;
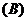
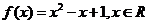 ,
,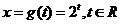 ;
;
(2)设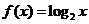 的值域
的值域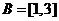 ,已知
,已知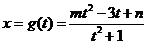 是
是 的一个
的一个 等值域变换,且函数
等值域变换,且函数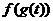 的定义域为
的定义域为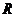 ,求实数
,求实数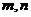 的值;
的值;
(3)设函数 的定义域为
的定义域为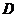 ,值域为
,值域为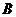 ,函数
,函数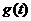 的定义域为
的定义域为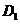 ,值域为
,值域为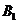 ,写出
,写出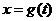 是
是 的一个等值域变换的充分非必要条
的一个等值域变换的充分非必要条
 件(不必证明),并举例说明条件的不必要性.
件(不必证明),并举例说明条件的不必要性.

[解](1)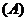 :函数
:函数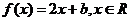 的值域为
的值域为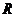 ,
,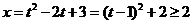 ,
,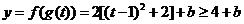 ,
,
所以,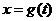 不是
不是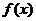 的一个等值域变换;
的一个等值域变换;
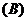 :
: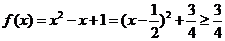 ,即
,即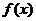 的值域为
的值域为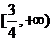 ,
,
当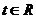 时,
时, ,即
,即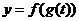 的值域仍为
的值域仍为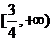 ,
,
所以,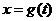 是
是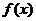 的一个等值域变换;
的一个等值域变换;
(2)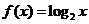 的值域为
的值域为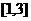 ,由
,由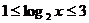 知
知 ,即
,即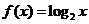 定义域为
定义域为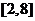 ,
,
因为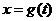 是
是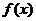 的一个等值域变换,且函数
的一个等值域变换,且函数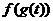 的定义域为
的定义域为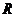 ,
,
所以,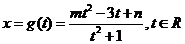 的值域为
的值域为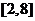 ,
,
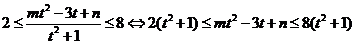 ,
,
所以,恒有 ,且存在
,且存在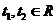 使两个等号分别成立,
使两个等号分别成立,
于是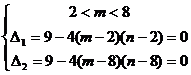 ,解得
,解得
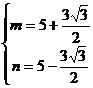 或
或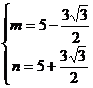
(3)设函数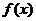 的定义域为
的定义域为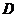 ,值域为
,值域为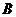
 ,函数
,函数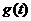 的定义域为
的定义域为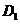 ,值域为
,值域为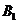 ,则
,则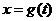 是
是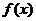 的一个等值域变换的充分非必要条件是“
的一个等值域变换的充分非必要条件是“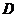 =
=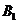 ”.
”.
条件的不必要性的一个例子是: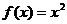 ,
,
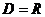 ,
,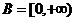

6.已知函数f(x)和g(x)的图像关于原点对称,且f(x)=x2+2x.
(1)求函数g(x)的解析式; (2)解不等式g(x)≥f(x)-|x-1|;
(3)若h(x)=g(x)-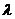 f(x)+1在[-1,1]上是增函数,求实数
f(x)+1在[-1,1]上是增函数,求实数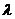 的取值范
的取值范 围.
围.
[思路分析](1)可利用f(x)和g(x)的图像关于原点对称,用求轨迹的方法求出g(x)的解析式,(2)是要解一个绝对值不等式,可通过讨论去掉绝对值符号,(3)是有关一个二次函数的单调性的讨论问题,可结合开口方向与对称轴的位置进行求解.
[解](1)设函数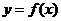 的图像上任一点
的图像上任一点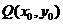 关于原点的对称点为
关于原点的对称点为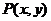 ,
,
则 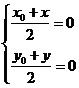 即
即 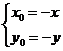 . ∵点
. ∵点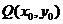 在函数
在函数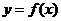 的图像上.
的图像上.
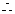
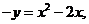 即
即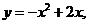 故g(x)=
故g(x)=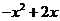 .
.
(2)由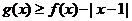 可得:
可得: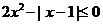 ,
,
当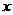
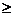 1时,
1时,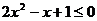 ,此时不等式无解.
,此时不等式无解.
当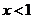
 时,
时, ,
,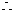
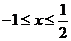
因此,原不等式的解集为[-1, 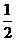 ].
].
(3) 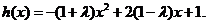
①
当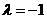 时,
时,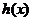 =
=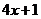 在[-1,1]上是增
在[-1,1]上是增 函数,
函数,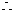
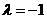
②当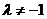 时,对称轴的方程为
时,对称轴的方程为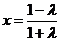
(i) 当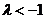 时,
时,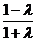
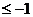 ,解得
,解得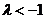 .
.
(ii) 当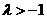 时,
时,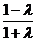
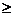 1时,解得
1时,解得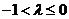
综上,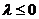
5. 某投资公司计划投资
某投资公司计划投资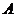 、
、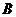 两种金融产
两种金融产 品,根据市场调查与预测,
品,根据市场调查与预测,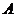 产品的利润与投资量成正比例,其关系如图1,
产品的利润与投资量成正比例,其关系如图1,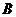 产品的利润与投资
产品的利润与投资 量的算术平方根成正比例,其关系如图2,(注:利润与投资量单位:万元).
量的算术平方根成正比例,其关系如图2,(注:利润与投资量单位:万元).
(1)分别将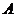 、
、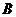 两产品的利润表示为投资量的函数关系式;
两产品的利润表示为投资量的函数关系式;
(2)该公司已 有10万元资金,并全部投入
有10万元资金,并全部投入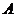 、
、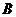 两种产品中,问:怎样分配这10万元投资,才能使公司获得最大
两种产品中,问:怎样分配这10万元投资,才能使公司获得最大 利润?其最大利润为多少万元?
利润?其最大利润为多少万元?
[解](1)设投资为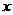 万元,
万元,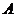 产品的利润为
产品的利润为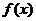 万元,
万元,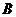 产品的利润为
产品的利润为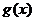 万元.由题意设
万元.由题意设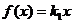 ,
,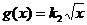 .由图可知
.由图可知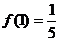 , ∴
, ∴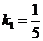 . 又
. 又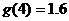 ,∴
,∴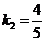 .
.
从 而
而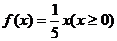 ,
,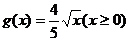 .
.
(2)设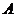 产品投入
产品投入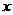 万元,则
万元,则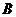 产品投入(
产品投入(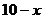 )万元,设企业利润为
)万元,设企业利润为 万元.
万元.
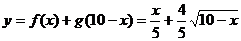
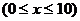 ,
,
令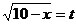 ,则
,则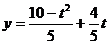
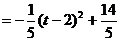
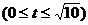 .
.
当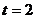 时,
时,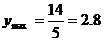 ,此时
,此时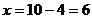 .
.
答:当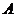 产品投入6万元,则
产品投入6万元,则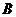 产品投入4万元时,该企业获得最大利润,利润为2.8万元.
产品投入4万元时,该企业获得最大利润,利润为2.8万元.
[点评]本题考察了函 数关系的建立及求最值的方法(换元法)等.同时,由于它是一个应用题,大家在写的时候要注意“答”,一定不要
数关系的建立及求最值的方法(换元法)等.同时,由于它是一个应用题,大家在写的时候要注意“答”,一定不要 丢.
丢.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com