
7.一元二次方程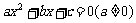 中,若a,b都是偶数,c是奇数,则这个方程( )
中,若a,b都是偶数,c是奇数,则这个方程( )
(A) 有整数根 (B) 没有整数根 (C) 没有有理数根 (D) 没有实数根
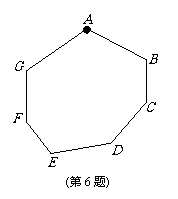
6.如图,一枚棋子放在七边形ABCDEFG的顶点A处,现顺时针方向移动这枚棋子10次,移动规则是:第k次依次移动k个顶点.如第一次移动1个顶点,棋子停在顶点B处,第二次移动2个顶点,棋子停在顶点D处.依这样的规则,在这10次移动的过程中,棋子不可能停到的顶点是( )
(A) C,E,F (B) C,E,G
(C) C,E (D) E,F
5.书架上有两套同样的教材,每套分上、下两册,在这四册教材中随机抽取两册,恰好组成一套教材的概率是( )
 (A)
(A) 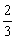 (B)
(B)
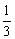 (C)
(C)
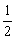 (D)
(D)
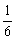
4.作抛物线A关于x轴对称的抛物线B,再将抛物线B向左平移2个单位,向上平移1个单位,得到的抛物线C的函数解析式是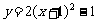 ,则抛物线A所对应的函数表达式是( )
,则抛物线A所对应的函数表达式是( )
(A) 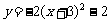 (B)
(B) 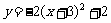
(C) 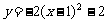 (D)
(D)
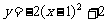
3.将长为15 dm的木棒截成长度为整数的三段,使它们构成一个三角形的三边,则不同的截法有( )
(A) 5种 (B) 6种 (C) 7种 (D) 8种
2.一块含30°角的直角三角板(如图),它的斜边AB=8cm,里面空心△DEF的各边与△ABC的对应边平行,且各对应边的距离都是1 cm,那么△DEF的周长是( )
(A)
5 cm (B) 6 cm
(C)(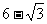 )cm (D)(
)cm (D)(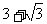 )cm
)cm
1. 要使方程组
要使方程组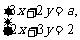 的解是一对异号的数,则a的取值范围是( )
的解是一对异号的数,则a的取值范围是( )
(A) 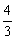 <a<3 (B) a<
<a<3 (B) a<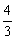 (C) a>3 (D) a<
(C) a>3 (D) a<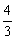 ,或a>3
,或a>3
25.已知在平面直角坐标系中,点C(O,2),D(3,4),在x轴上有一点A,它到点C、
点D的距离之和最小。
(1) 求过点C、A、D的抛物线的解析式
(2) 设(1)中抛物线与x轴的另一个交点为B,求四边形CABD的面积;
(3) 把(1)中的抛物线先向左平移一个单位,再向上或向下平移多少个单位能使抛物
线与直线AD只有一个交点?
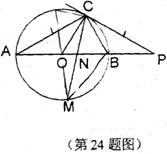
24.已知:如图,已知点C在圆0上,P是圆0外一点,
割线PO交圆O于点B、A,已知AC=PC,
∠COB=2∠PCB,且PB=2
(1)求证:PC是圆O的切线;
(2)求:tan∠P:
(3)M是圆0的下半圆弧上的一动点,当M点运动到使△ABM的面积最大时,
连接CM交AB于点N,求MN·MC的值.
23.已知:直线y=-2x+10与x轴、y轴分别交于A、B两点,
把△AOB以AB为轴翻折,原点O落在点C处
(1)求A、B两点的坐标
(2)求点C到x轴的距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com