
24.(本题满分9分) 如图(1)是网格中的一副七巧板,用它可以拼出13种不同的凸多边形,图(2)是在网格中,用图(1)中的七巧板拼出的一个平行四边形.请你再在图(3)的网格中,用图(1)中的七巧板拼出一个的六边形(请将拼出的六边形用铅笔涂黑,并标上七巧板的标号).

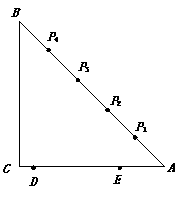
23、(本题满分8分)如图,△ABC中,AC=BC=5 ,
∠C=90°,P1, P2, P3, P4是AB的五等分点,线段DE在边AC上移动,DE=3.请问:在线段DE的移动过程中,四边形P1P3DE的周长是否有最小值?若有,求出这个最小值和这时CD的长;若没有,说明理由.
22.(本题满分8分)直线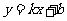 经过点B(0,2),抛物线
经过点B(0,2),抛物线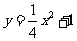
(1)将直线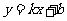 绕点B旋转到与x轴平行的位置时(如图①),直线与抛物线
绕点B旋转到与x轴平行的位置时(如图①),直线与抛物线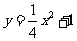 相交,其中一个交点为P,求点P的坐标;
相交,其中一个交点为P,求点P的坐标;
(2)将直线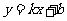 继续绕点B旋转,与抛物线
继续绕点B旋转,与抛物线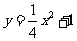 相交,其中一个交点为P'(如图②),过点P'作x轴的垂线P'M,点M为垂足.是否存在这样的点P',使△P'BM为等边三角形?若存在,请求出点P'的坐标;若不存在,请说明理由.
相交,其中一个交点为P'(如图②),过点P'作x轴的垂线P'M,点M为垂足.是否存在这样的点P',使△P'BM为等边三角形?若存在,请求出点P'的坐标;若不存在,请说明理由.
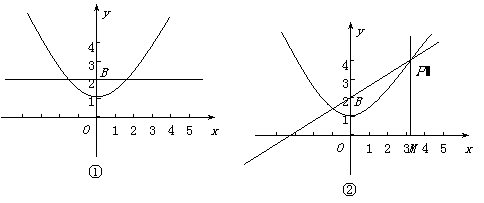
21. (本题满分8分) 直线l1: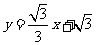 分别交x, y轴于点A , C , l2:
分别交x, y轴于点A , C , l2: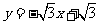 分别交x , y轴于点B , C
分别交x , y轴于点B , C
(1)求A、B、C的坐标.
(2)把△ABC绕AB的中点M旋转180°,得到四边形AEBC.
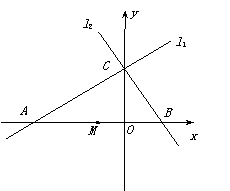 ①求E点坐标.
①求E点坐标.
②试判断四边形AEBC的形状,并说明理由.
20.(本题满分8分)(1) 已知四个互不相等的实数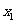 ,
,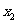 ,
,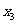 ,
,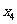 ,其中
,其中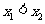 ,
,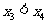 .请将
.请将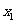 ,
,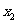 ,
,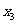 ,
,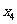 从小到大排列起来.
从小到大排列起来.
(2)设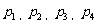 是不等于零的有理数,
是不等于零的有理数,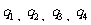 是无理数,下列四个数①
是无理数,下列四个数①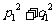 ,②
,②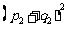 ,③
,③ ,④
,④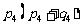 必为无理数的是 (只写出序号);可以是有理数的是 (只写出序号);若该数是有理数请举出一个特例说明.
必为无理数的是 (只写出序号);可以是有理数的是 (只写出序号);若该数是有理数请举出一个特例说明.
18.(本题满分9分)(1) 为了了解市场上甲、乙两种手表日走时误差的情况,从这两种手表中各随机抽取10块进行测试,两种手表日走时误差的数据如下(单位:秒)
 编 号 编 号类 型 |
一 |
二 |
三 |
四 |
五 |
六 |
七 |
八 |
九 |
十 |
|
甲种手表 |
-3 |
4 |
2 |
-1 |
-2 |
-2 |
1 |
-2 |
2 |
1 |
|
乙种手表 |
-4 |
1 |
-2 |
1 |
4 |
1 |
-2 |
-1 |
2 |
-2 |
①计算甲、乙两种手表日走时误差的平均数;
②你认为甲、乙两种手表中哪种手表走时稳定性好?说说你的理由.
(2)某种饮料每箱装6听,如果其中有2听不合格,问质检人员从中随机抽出2听,检验出产品不合格的概率有多大?(画出数状图求概率)

19(本题满分8分)(1)如图 ,凸八边形ABCDEFGH的八个内角都相等,边AB=7,BC=4,CD=2,DE=5,EF=6,FG=2,
求该八边形的周长.

(2)如图,图中的虚线网格我们称为“正三角形网格”,它的每一个小三角形都是边长为1的正三角形,这样的三角形称为“单位正三角形”.求图中的格点四边形ABCD的面积.

17、如图,Rt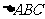 中,
中,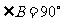 ,
,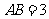 ,
,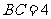 ,
,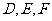 分别是三边
分别是三边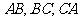 上的点,则
上的点,则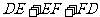 的最小值为
.
的最小值为
.
16、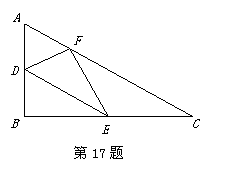
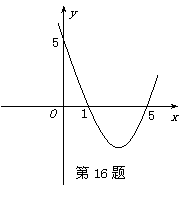 抛物线
抛物线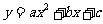 的部分图像如图所示,则该抛物线的对称轴为直线 ;满足y<0的x取值范围是 ;将抛物线
的部分图像如图所示,则该抛物线的对称轴为直线 ;满足y<0的x取值范围是 ;将抛物线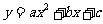
平移 个单位,则得到抛物线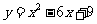
15、 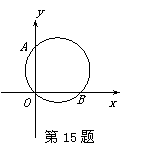 如图,在直角坐标系中,P是经过点O(0,0),A(0,2),B(2,0)的圆上一个动点(点P与点O,B不重合)则∠OPB= 度.
如图,在直角坐标系中,P是经过点O(0,0),A(0,2),B(2,0)的圆上一个动点(点P与点O,B不重合)则∠OPB= 度.
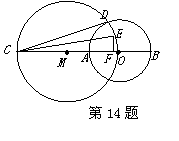
14、如图,AB是⊙O的直径,点C在BA的延长线上,以OC为直径的⊙M与⊙O 交于点D,∠DCB的平分线与⊙M交于点E,作EF⊥AB于点F,若⊙O的半径为5,
则EF=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com