
3、如图所示的方格纸中,每个小正方形的边长都为1,如果以MN所在的直线为y轴,以小正方形的边长为单位长度建立平面直角坐标系,使A点与B点关于原点对称,则这时C点的坐标可能是
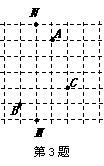 A、(1,3)
B、(2,-1)
A、(1,3)
B、(2,-1)
C、(2,1) D、(3,1)
2、下列方程中,有实数根的是
A、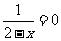 B、
B、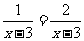
C.、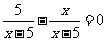 D、
D、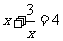
1、下列各数与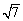 最接近的是
最接近的是
A、 2.5 B、 2.6 C、 2.7 D、 2.8
26.(本小题满分12分)
某小区要在一块矩形空地.ABCD上建造一个矩形公园GHCK,为了使小区内的文物保护区△AEF不被破坏,矩形公园的顶点G不能在文物保护区内.已知AB=200m,AD=160m,AE=40m,AF=60m.
(1)当矩形小区公园的顶点G恰好是线段EF的中点时,求公园区域的面积;
(2)当G在线段EF上移动时,设GH=xm,矩形公园GHCK的面积为ym2,
①写出y与x之间的函数关系式;
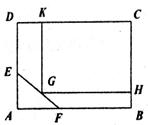 ②是否某一个时刻,矩形公园GHCK的面积取得最大值,若存在求出此时x的值;若不存在,说明理由.
②是否某一个时刻,矩形公园GHCK的面积取得最大值,若存在求出此时x的值;若不存在,说明理由.
25.(本小早满分10分)
某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨1元,月销售量就减少10千克.针对这种水产 品的销售情况,请回答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;
(2)设销售单价定为每千克x元,月销售利润为y元,求y与x的函数解析式;
(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?(单价是整数)
24.(本小题满分8分)
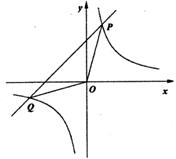 如图,已知反比例函数y=
如图,已知反比例函数y=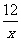 的图象与一次函数y=kx+4的图象相交于P、Q两点,并且P点的纵坐标是6.
的图象与一次函数y=kx+4的图象相交于P、Q两点,并且P点的纵坐标是6.
(1)求这个一次函数的解析式。
(2)求△POQ的面积.
23.(本小题满分8分)
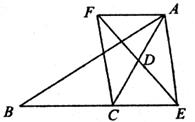
已知;如图,在△ABC中,D是AC的中点,E是线段BC延长线上一点,过点A作BE的平行线与线段ED的延长线交于点F,连接AE、CF.
(1)求证:AF=CE
(2)若AC=EF,试判断四边形AFCE是什么样的四边形?并证明你的结论.
22.(本小题满分8分)
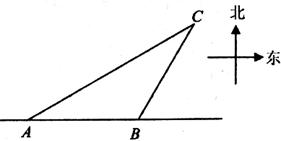 如图,一艘渔船正以30km/h的速度由西向东行驶,在一处看见小岛C在船的北偏东60
如图,一艘渔船正以30km/h的速度由西向东行驶,在一处看见小岛C在船的北偏东60 .4min后,渔船行至B处,此时看见小岛C在船的北偏东30
.4min后,渔船行至B处,此时看见小岛C在船的北偏东30 .已知以小岛C为中心周围1km以内为某渔业公司承包的养殖区域.若这艘渔船继续向东行驶,是否有可能进入该养殖区域?
.已知以小岛C为中心周围1km以内为某渔业公司承包的养殖区域.若这艘渔船继续向东行驶,是否有可能进入该养殖区域?
21.(本小题满分6分)
A、B两个口袋中均有3个分别标有数字1、2、3的完全相同的球,甲、乙两人进行摸球游戏.游戏规则是:甲从A袋中随机摸一个球,乙从B袋中随机摸一个球,当两个球上所标数字之和为奇数时,则甲赢,否则乙赢.问这个游戏公平吗?为什么?
20.(本小题满分6分)
已知关于x的一元二次方程kx2-2x+k2=0的两个实根分别为O和a,求a及k的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com