
22.(本小题满分8分)
如图1,图2,四边形ABCD是正方形,M是AB延长线上一点.直角三角尺的一条直角边经过点D,且直角顶点E在AB边上滑动(点E不与点A,B重合),另一条直角边与∠CBM的平分线BF相交于点F.

(1)如图1,当点E在AB边的中点位置时:
①通过测量DE,EF的长度,猜想DE与EF满足的数量关系是______________;
②连接点E与AD边的中点N,猜想NE与BF满足的数量关系是________________;
③请证明你的上述两猜想.
(2)如图2,当点E在AB边上的任意位置时,请你在AD边上找到一点N,使得NE=BF,进而猜想此时DE与EF有怎样的数量关系.
20.(本小题满发8分)已知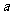 、
、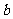 为实数,且
为实数,且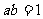 ,设
,设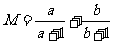 ,
,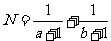 ,试用两种方法比较M、N的大小.
,试用两种方法比较M、N的大小.
19.(本小题满分8分)如图,已知三角形ABC,其中AB=AC.
(1)作AB的垂直平分线DE,交AB于D点,AC于E点;连结BE{尺规作图,不写作法,保留作图痕迹)
(2)在(1)的基础上,若AB=8,三角形BCE的周长为14,求BC的长.
18.若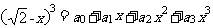 ,则
,则

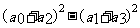 的值为______.
的值为______.
17.假设一家旅馆一共有30个房间,分别编以1--30三十个号码,现在要在每个房间的钥匙上刻上数字,要求所刻的数字必须使服务员很容易辨认是哪一个房间的钥匙,而使局外人不容易猜到.现在有一种编码的方法是:在每把钥匙上刻上两个数字,左边的一个数字是这把钥匙原来的房间号码除以5所得的余数,而右边的一个数字是这把钥匙原来的房间号码除以7所得的余数.那么刻的数是36的钥匙所对应的原来房间应该是__________号.
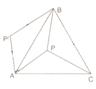
16.如图,P是等边三角形ABC内一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后,得到△P′AB,则点P与点P′之间的距离是_________,∠APB=________.
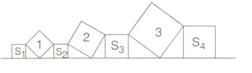
15.在直线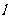 上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积依次为1,2,3,正放置的四个正方形的面积依次为S1,S2,S3,S4,则S1+S2+S3+S4=________.
上依次摆放着七个正方形(如图所示).已知斜放置的三个正方形的面积依次为1,2,3,正放置的四个正方形的面积依次为S1,S2,S3,S4,则S1+S2+S3+S4=________.
14.如果记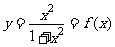 ,并且
,并且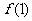 表示
表示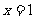 时,
时, 的值,即,
的值,即,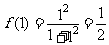 ;
;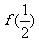 表示
表示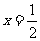 时
时 的值,即
的值,即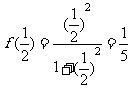 ,那么
,那么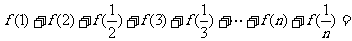 ________.(结果用含
________.(结果用含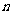 的代数式表示,
的代数式表示,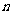 为正整数)
为正整数)
13.某电视台在黄金时段的2分钟广告时间内,计划插播长度为15秒和30秒的两种广告.15秒的广告每播一次收费0.6万元,30秒的广告每播一次收费1万元.若要求每种广告播放不少于2次,则电视台在播放时最大收益是_________万元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com