
3.刘翔在出征雅典奥运会前刻苦进行110米跨栏训练,教练对他10次的训练成绩进行统计分析,判断他的成绩是否稳定,则教练需要知道刘翔这10次成绩的
A. 众数 B.方差 C.平均数 D.频数
2.下列运算中正确的是
A.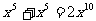 B.
B.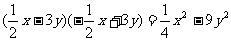
C.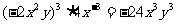 D.
D.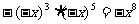
1.如图,数轴上所标出的点中,相邻两点间的距离相等,则点A表示的数为

A.30 B.50 C.60 D.80
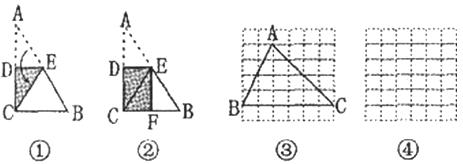
25.(本题满分14分)
(1)图①是一块直角三角形纸片.将该三角形纸片按如图①方法折叠,其中点A与点C重合,DE为折痕.试证明△CBE是等腰三角形;
(2)再将图①中的△CBE沿对称轴EF折叠(如图②).通过折叠,原三角形恰好折成两个重合的矩形,其中一个是内接矩形,另一个是拼合(指无缝无重叠)所成的矩形,我们称这样的两个矩形为“组合矩形”.你能将图③中的△ABC折叠成一个组合矩形吗?如果能折成,请在图③中画出折痕;
(3)请在图④的方格纸中画出一个斜三角形,同时满足下列条件:①折成的组合矩形为正方形;②顶点都在格点(各小正方形的顶点)上;
(4)有一些特殊的四边形,如菱形,通过折叠也能折成组合矩形(其中的内接矩形的四个顶点分别在原四边形的四条边上).请你进一步探究,一个非特殊的四边形(指除平行四边形、梯形外的四边形)满足何条件时,一定能折成组合矩形?
24.(本题满分12分)
已知抛物线y=ax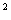 +bx+c与y轴交于A(0,3),与x轴分别交于B(1,0)、C(5, 0)两点.
+bx+c与y轴交于A(0,3),与x轴分别交于B(1,0)、C(5, 0)两点.
(1)求此抛物线的解析式;
(2)若一个动点P自OA的中点M出发先到达x轴上的某点(设为点E),再到达抛物线的对称轴上某点(设为点F),最后运动到点A,求使点P运动的总路径最短的点E、点F的坐标,并求出这个最短总路径的长.
23.(本题满分10分)
一长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD边上(如图).
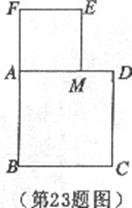
(1)求AM、MD的长;
(2)你能说明点M是线段AD的黄金分割点吗?
22.(本题满分10分)
如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等份,每份分别标上l,2,3,4四个数字;转盘B被均匀地分成6等份,每份分别标上l,2,3,4,5,6六个数字,有人为甲、乙两人设计了一个游戏,其规则如下:
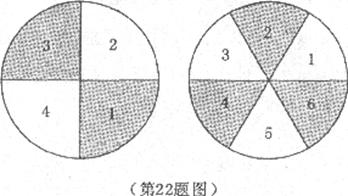
(1)同时自由转动转盘A与B;
(2)转盘停止后,指针各指向一个数字(如果指针恰好指在分格线上,那么重转一次,直到指针指向某一数字为止),用所指的两个数作乘积,如果得到的积是偶数,那么甲胜;如果得到的积是奇数,那么乙胜(如转盘A指向3,转盘B指针指向5,3×5=15,按规则乙胜).你认为这样的规则是否公平?请说明理由;如果不公平,请你设计一个公平的规则,并说明理由.
21.(本题满分10分)
某单位想为每名职工买一个电热水壶,采购员获得的信息是:甲、乙、丙三家商场均有销售同一牌子的电热水壶,并且各有自已的优惠办法.甲商场每个电热水壶定价100元,九折;买10个以上可以八折;买50个以上可以七折.乙商场每个电热水壶定价90元,九折;买10个以上可以八五折;买50个以上可以八折.丙商场每个电热壶定价为78元,不打折.请你为采购员设计方案,究竟在哪一家买更合算?
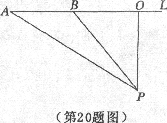
20.(本题满分10分)
如图已知测速站P到公路L的距离PO为40米,一辆汽车在公路L上行驶,测得此车从A到B所用时间为2秒,并测得∠APO=60°,∠BPO=40°,计算此车从A到B的平均速度为每秒多少米?(结果保留四位有效数字)并判断此车是否超过了每秒22米的限制速度?
19.(本题满分8分)
如图四个条件中,请你以其中两个为已知条件,第三个为结论,推出一个正确的命题(只需写出一种情况)写出证明过程
①AE=AD,②AB=AC,③OB=OC,④∠B=∠C.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com