
1.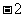 的相反数是
的相反数是
A.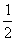 B.
B.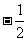 C.
C.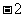 D.
D.
25.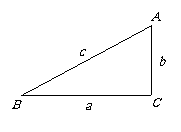 在△ABC中,∠A、∠B、∠C所对的边分别用a、b、c表示。
在△ABC中,∠A、∠B、∠C所对的边分别用a、b、c表示。
(1)如图,在△ABC中,∠A=2∠B,且∠A=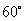 .
.
求证:a2=b(b+c).
证明:
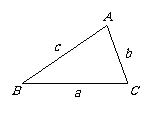
(2)如果一个三角形的一个内角等于另一个内角的2 倍,我们称这样的三角形为“倍角三角形”.(1)中的三角形是一个特殊的倍角三角形,那么对于任意的倍角三角形ABC,其中∠A=2∠B,关系式a2=b(b+c)是否仍然成立?若成立,证明你的结论;若不成立,请说明理由.
 解:
解:
(3)试求出一个倍角三角形的三条边的长,使这三条边长恰为三个连续的正整数.
解:
24. 如图,在平面直角坐标系中,Rt△AOB的顶点坐标分别为A(-2,0),O(0,0),B(0,4),
把△AOB绕点O按顺时针方向旋转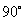 ,得到△COD.
,得到△COD.
(1)求C、D两点的坐标;
(2)求经过A、B、D三点的抛物线的解析式;
 (3)在(2)中的抛物线的对称轴上取两点E、F(点E在点F的上方),且EF=1,使四边形ACEF 的周长最小,求出E、F两点的坐标.
(3)在(2)中的抛物线的对称轴上取两点E、F(点E在点F的上方),且EF=1,使四边形ACEF 的周长最小,求出E、F两点的坐标.
解:
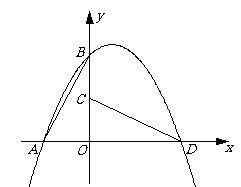
23.如图,某学校要建一个中间有两道篱笆隔断的长方形花圃,花圃的一边靠墙(墙的最大可利用长度为10m),现有篱笆长24m.设花圃的宽AB为x m,面积为S m2.
(1)求S与x之间的函数关系式;
(2)如果要围成面积为32m2的花圃, AB的长是多少米?
(3)能围成面积比32m2更大的花圃吗? 如果能,请求出最大面积,并给出设计方案;
 如果不能,请说明理由.
如果不能,请说明理由.
解:
22.已知直线l1 :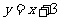 与 l2 :
与 l2 :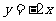 交于点B, 直线l1 与x轴交于点A, 动点P在线段OA上移动(不与点A、O重合) .
交于点B, 直线l1 与x轴交于点A, 动点P在线段OA上移动(不与点A、O重合) .
(1) 求点B的坐标;
(2) 过点P作直线l与x轴垂直, 设P点的横坐标为x, △ABO中位于直线l左侧部分的面积为S, 求S与x之间的函数关系式.
解:
21. 为了了解学生参加体育活动的情况,某中学对学生进行了随机抽样调查,其中一个问题是 “你平均每天参加体育活动的时间是多少?”,共有4个选项:
A.1.5小时以上 B.1-1.5小时 C.0.5-1小时 D.0.5小时以下
下图是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:
(1)本次一共调查了多少名学生?
(2)在图①中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
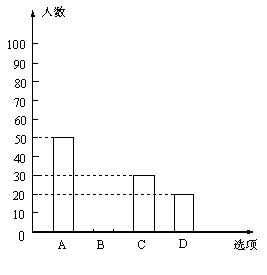
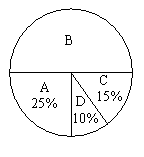
图① 图②
解:
20. 如图,矩形纸片ABCD是由24个边长为1的正方形排列而成, M是AD的中点.
(1)沿虚线MB剪开,分成两块纸片进行拼图.
要求: ①拼成直角三角形; ②拼成平行四边形; ③拼成等腰梯形.
将所拼图形画在相应的网格中.
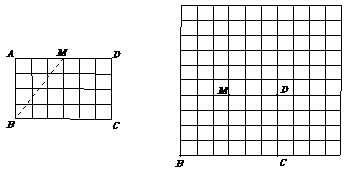
① 拼成直角三角形
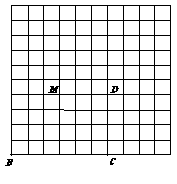
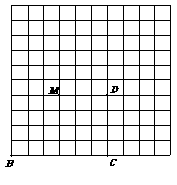
② 拼成平行四边形 ③ 拼成等腰梯形
(2) 能否将矩形ABCD剪 (限剪两刀) 拼成菱形?若能,请利用下面的网格设计剪拼图案(画出分割线即可)并写出相应的菱形的边长;若不能,请简要说明理由.

19. 已知:如图,AB是⊙O的直径, ⊙O过BC的中点D,且DE⊥AC于点E.
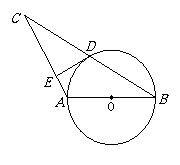 (1)求证:DE是⊙O的切线;
(1)求证:DE是⊙O的切线;
(2)若∠C=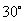 , CD=10cm, 求⊙O的直径.
, CD=10cm, 求⊙O的直径.
(1)证明:
(2)解:
18.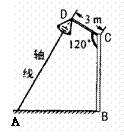 如图,要在宽为28m的海堤公路的路边安装路灯.路灯的灯臂长为3 m,且与灯柱成
如图,要在宽为28m的海堤公路的路边安装路灯.路灯的灯臂长为3 m,且与灯柱成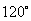 角,路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直.当灯罩的轴线通过公路路面的中线时,照明效果最理想.问:应设计多高的灯柱,才能取得最理想的照明效果(精确到0.01).
角,路灯采用圆锥形灯罩,灯罩的轴线与灯臂垂直.当灯罩的轴线通过公路路面的中线时,照明效果最理想.问:应设计多高的灯柱,才能取得最理想的照明效果(精确到0.01).
解:
17.已知关于x的一元二次方程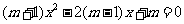 有实数根,求m的取值范围.
有实数根,求m的取值范围.
解:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com