
2.下列各式运算正确的是( )
A.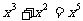 B.
B.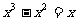
C.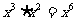 D.
D.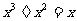
1.-5的相反数是( )
A.5 B.5 C.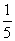 D.
D.
28.(本题满分l2分)
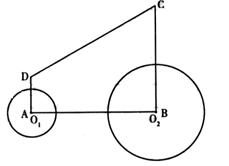
如图,在直角梯形ABCD中,AD∥BC,∠A=90°,∠C=60°,AD=3cm,BC=9cm,⊙O1的圆心O1从点A开始沿折线A-D-C以1cm/s的速度向点C运动,⊙O2的圆心O2从点B开始沿BA边以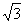 cm/s的速度向点A运动,⊙O1的半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为
cm/s的速度向点A运动,⊙O1的半径为2cm,⊙O2的半径为4cm,若O1、O2分别从点A、点B同时出发,运动的时间为 s。
s。
(1)请求出⊙O2与腰CD相切时 的值;
的值;
(2)在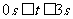 范围内,当
范围内,当 为何值时,⊙O1与⊙O2外切?
为何值时,⊙O1与⊙O2外切?
27.(本题满分l0分)
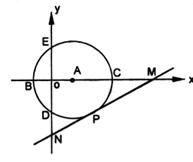
如图,在直角坐标系中,以点A(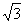 ,0)为圆心,以
,0)为圆心,以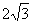 为半径的圆与
为半径的圆与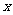 轴交于B、C两点,与
轴交于B、C两点,与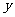 轴交于D、E两点。
轴交于D、E两点。
(1)求D点坐标。
(2)若B、C、D三点在抛物线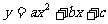 上,求这个抛物线的解析式。
上,求这个抛物线的解析式。
(3)若⊙A的切线交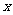 轴正半轴于点M,交
轴正半轴于点M,交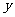 轴负半轴于点N,切点为P,
轴负半轴于点N,切点为P,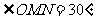 ,试判断直线MN是否经过所求抛物线的顶点?说明理由。
,试判断直线MN是否经过所求抛物线的顶点?说明理由。
26.(本题满分l0分)
我们知道:顶点在圆上,并且两边都和圆相交的角叫做圆周角,一条弧所对的圆周角的度数等于它所对的圆心角度数的一半。类似地,我们定义:顶点在圆外,并且两边都和圆相交的角叫做圆外角。
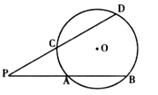
(1)判断:图中有没有圆外角?如果有,请用字母表示出来。
(2)运用所学的数学知识,探究:圆外角的度数与它所夹的弧所对的圆心角的度数有什么关系?将你的发现,用文字表述出来,并说明理由。
24.(6分)
某商厦张贴巨幅广告:“真情回报顾客”活动共设奖金20万元,最高奖每份1万元,平均每份奖金200元,一顾客幸运地抽到一张奖券,奖金数为10元,她调查了周围正兑奖的其他顾客,一个也没有超过50元的,她气愤地要求与商厦领导评理。商厦领导说不存在欺骗,并向她出示了下面这张奖金分配表,你认为商厦说“平均每份奖金200元”是否欺骗了顾客?大多数中奖者获得的奖金能接近奖金的平均数吗?中一等奖的概率是多少?以后遇到开奖的问题你应该更关心什么?
|
奖金等级 |
一等奖 |
二等奖 |
三等奖 |
四等奖 |
五等奖 |
|
奖金额(元) |
10000 |
6000 |
1000 |
50 |
10 |
|
中奖人数 |
3 |
10 |
87 |
350 |
550 |
23.(本题满分8分)
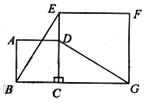
如图,正方形ABCD的边CD在正方形ECGF的边CE上,连结BE、DG。
(1)观察猜想BE与DG之间的大小关系,并证明你的结论。
(2)图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说出旋转过程;若不存在,请说明理由。
22.(6分)
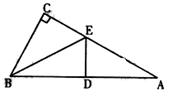
如图,在Rt△ABC中,∠C=90°,沿过点B的直线BE折叠这个三角形,要使点C恰好与AB的中点D重合,还应添加什么条件?
21.(4分)
计算: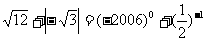
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com