23．(本小题8分)

某运动员在距离篮下4米处跳起投篮，球的运行路线是抛物线的一部分，当球运行的水平距离为2.5米时，到达最大离度3.5米，然后准确落入篮筐；已知篮圈中心到地面的距离为3.05米，该运动员的身高为l.80米。

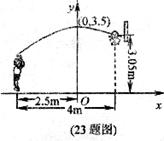
(1)建立如图所示的坐标系，求抛物线的解析式。

(2)在这次跳起投篮中，球在头顶上方0.25米处出手，那么它在球出手时跳离地面多高？

22．(本小题8分)

本商店积压了l00件某种商品，为使这批货物尽快出售，该商店采取了如下销售方案，先将价格提高到原来的2.5倍，再作三次降价处理：第一次降价30%标出了“亏本价”，第二次降价30%，标出“破产价”，第三次又降价30%，标出“跳楼价”，三次降价处理销售情况如下表。

问：(1)跳楼价占原价的百分比是多少？

(2)该商品按新销售方案销售，相比原价全部售完，哪一种方案更盈利，请通过计算加以说明。

21．(本小题8分)

如图，在5×5的正方形网格中，每个小正方形的边长都为1，请在所给网格中按下列要求画出图形。

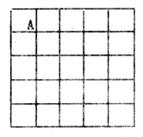
(1)从点A出发的一条线段AB，使它的另一个端点落在格点(即小正方形的顶点)上，且长度为；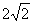

(2)以(1)中的AB为边的一个等腰三角形ABC，使点C在格点上，且另两边的长都是无理数；

(3)以(1)中的AB为边的一个凸多边形，使它是中心对称图形，其顶点都在格点上，各边长都是无理数。

20．(本小题7分)

如图，正方形ABCD和正方形EFGH的边长分别为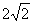和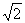，对角线BD、FH都在直线L上，O₁、O₂分别是正方形的中心。线段O₁O₂的长叫做两个正方形的中心距。当中心O₂在直线L上平移时，正方形EFGH也随平移，在平移时正方形EFGH的形状、大小没有改变。

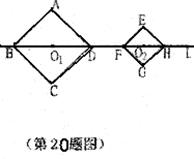
(1)计算：O_lD=__________，O₂F=__________。

(2)当中心O₂在直线L上平移到两个正方形只有一个公共点时，中心距O₁O₂=________。

(3)随着中心O₂在直线L上的平移，两个正方形的公共点的个数还有哪些变化？并求出相对应的中心距的值或取值范围(不必写出计算过程)。

19．(本小题5分)

化简：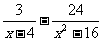

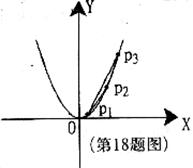
18．小明设计了一个电子游戏：一电子跳蚤从抛物线上横坐标为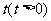的P₁点开始，按点的横坐标依次增加1的规律，在抛物线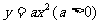上向右跳动，得到点P₂、P₃，这时△P₁P₂P₃的面积为__________。

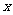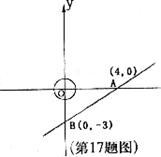
17．直角坐标系中直线AB分别交轴、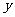轴于点A(4，0)与B(0，-3)，现有一半径为1 的动圆的圆心位于原点处，以每秒1个单位的速度向右作平移运动，则经过________秒后动圆与直线AB相切。

16．如图，用同样规格的黑白两色的正方形瓷砖铺设矩形地面，请观察图形并解答下列问题。

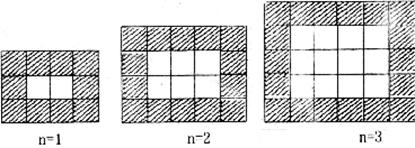
在第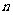个图中，共有__________白块瓷砖(用含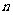的代数式表示)。

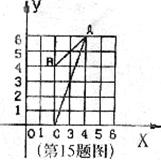
15．如图，△ABC的外接圆的圆心坐标为__________。

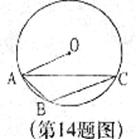
14．如图，A、B、C为⊙O上三点，∠ACB=20°，则∠BAO的度数为__________°。