1．刘强和王兵在教室里的位置可以用点(4，1)和点(2，7)表示，(4，1)中的4表示第4列，(2，7)表明王兵坐在第______行第______列。

　　 已知抛物线与y轴的交于C点，C点关于抛物线对称轴的对称点为C′

(1)求抛物线的对称轴及C、C′的坐标(可用含m的代数式表示)：

(2)如果点Q载抛物线的对称轴上，点P在抛物线上，以点C、C′、P、Q为顶点的四边形是平行四边形，求Q点和P的坐标(可用含m的代数式表示)

设这种面包的单价为(角)，零售店每天销售这种面包所获得的利润为(角)．

(1)用含的代数式分别表示出每个面包的利润与卖出的面包个数；

(2)求与之间的函数关系式；

(3)当面包单价定位多少时，该零售店每天销售这种面包获得的利润最大？最大利润为多少？

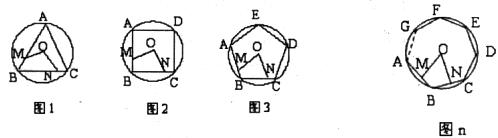
如图l、2、3、…、n，M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点，且BM=CN，连结OM、ON．

(1)求图l中∠MON的度数：

(2)图2中∠MON的度数是________，图3中∠MON的度数是________；

(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案)．

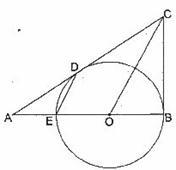
　　 如图，CB、CD是⊙O的切线，切点分别为B、D．CD的延长线与⊙O的直径BE的延长线交于A点，连结OC，ED．探索OC与ED的位置关系，并加以证明．

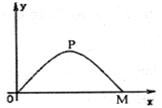　　　 施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为l2米．现以O点为原点，OM所在直线为轴建立直角坐标系(如图所示)．

　　 (1)直接写出点M及抛物线顶点P的坐标；

(2)求出这条抛物线的函数解析式．

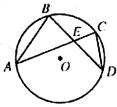
如图，在⊙O中，弦AC与BD交于E，AB=6，AE=8，ED=4．求CD的长．

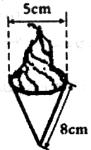
10．如图，冰淇淋蛋筒下部呈圆锥形，则蛋筒圆锥部分包装纸的面积(接缝处的部分忽略不计)是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　　(　　 )

(A)20cm²　　　　　　　 (B)40cm²　　　 (C)20cm² 　　　 (D)40cm²

9．如图，PA,PB是⊙O的两条切线，切点是A、B．如果OP=4，PA=2，那么∠AOB等于(　　 )

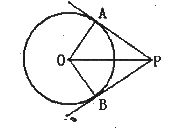
　　 (A)90°　 　　　　　　 　(B)100°　 　 　(C)110°　 　　　 　(D)120°

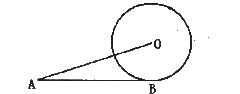
8．如图，AB与⊙O切于点B，AO=6 cm，AB=4 cm，则⊙O的半径为　　　 　　　　　(　　 )

　　 (A) 4cm　　 (B)cm　　 (C) 2 cm　　 (D) cm