
19.在一次晚会上,大家围着飞镖游戏前,看见靶子设计成下图形式,已知从里到外的三个圆的半径分别为l,2,3并且形成A,B,C三个区域.如果飞镖没有停落在最大圆内或只停落在圆周上,那么可以重新投镖.(本题满分8分)
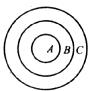
(1)分别求出三个区域的面积;
(2)甲与乙约定:飞镖停落在A、B区域甲得l分,飞镖落在C区域乙 得l分.你认为这个游戏公平吗?为什么?如果不公平,请你修改得分规则,使这个游戏公平.
18.在一块长16m、宽l2m的矩形荒地上,要建造一个学生实验植物园,要求植物园所占面积为荒地面积的一半,下面分别是小明和小颖的设计方案.(本题满分10分)
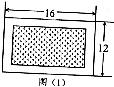
王明说:我的设计方案如图(1),其中园地四周小路的宽度相等.通过解方程,我得到小路的宽为2m或12m.
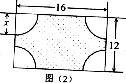
李颖说:我的设计方案如图(2),其中植物园为阴影部分,荒地的每个角上的扇形相同.
(1)你认为王明的结果对吗?请说明理由;
(2)请你帮助李颖求出图中的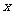 (精确到0.1m);
(精确到0.1m);
(3)你还有其他的设计方案吗?请在下边的矩形中画出你的设计草图,并加以说明.
17.下图,在Rt△ABC中,∠B=90°,∠A的平分线交BC于D,E为AB上一点,DE=DC,以D为圆心,以DB的长为半径画圆.
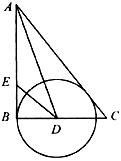
求证:(1)AC是⊙D的切线: (2)AB+EB=AC.
16.(1)计算: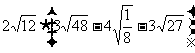 .
.
(2)当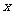 为何值时,
为何值时,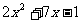 的值与
的值与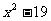 的值互为相反数.
的值互为相反数.
(本小题满分l0分)
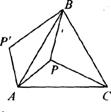
15.下图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△P′AB.则∠APB=_____________.
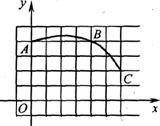
14.下图,直角坐标系中一条圆弧经过网格点A、B、C,其中B点坐标为(4,4),则该弧所在圆心的坐标是____________.
13.直线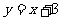 上有一点
上有一点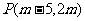 ,则
,则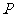 点关于原点的对称点
点关于原点的对称点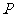 ′为__________.
′为__________.
12.若关于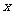 的一元二次方程
的一元二次方程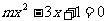 有两个不相等的实数根,则
有两个不相等的实数根,则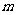 的取值范围是_________.
的取值范围是_________.
11.已知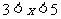 ,化简
,化简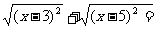 _________.
_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com