
1.下列由左到右的变形是因式分解的是( )
A.5x(x-1)=5x2-5x
B.2x2-3x+1=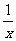 (2x3-x2+x)
(2x3-x2+x)
C.t2-16+3t=(t+4)(t-4)+3t D.y2-4y+4=(y-2)2
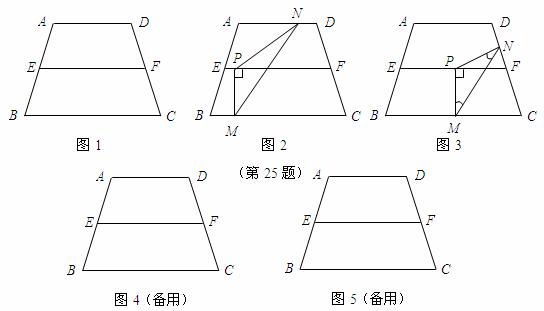
25.如图1,在等腰梯形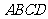 中,
中,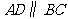 ,
,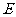 是
是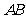 的中点,过点
的中点,过点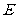 作
作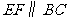 交
交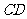 于点
于点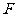 .
.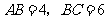 ,
,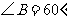 .
.
(1)求点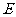 到
到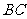 的距离;
的距离;
(2)点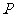 为线段
为线段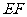 上的一个动点,过
上的一个动点,过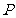 作
作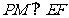 交
交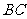 于点
于点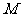 ,过
,过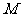 作
作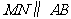 交折线
交折线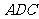 于点
于点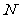 ,连结
,连结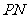 ,设
,设 .
.
①当点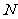 在线段
在线段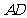 上时(如图2),
上时(如图2),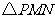 的形状是否发生改变?若不变,求出
的形状是否发生改变?若不变,求出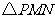 的周长;若改变,请说明理由;
的周长;若改变,请说明理由;
②当点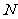 在线段
在线段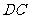 上时(如图3),是否存在点
上时(如图3),是否存在点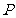 ,使
,使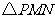 为等腰三角形?若存在,请求出所有满足要求的
为等腰三角形?若存在,请求出所有满足要求的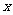 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
24.如图,抛物线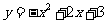 与
与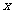 轴相交于
轴相交于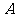 、
、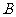 两点(点
两点(点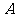 在点
在点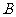 的左侧),与
的左侧),与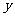 轴相交于点
轴相交于点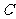 ,顶点为
,顶点为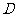 .
.
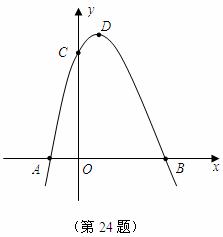
(1)直接写出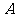 、
、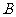 、
、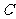 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
(2)连接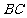 ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点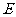 ,点
,点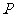 为线段
为线段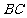 上的一个动点,过点
上的一个动点,过点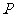 作
作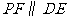 交抛物线于点
交抛物线于点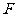 ,设点
,设点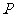 的横坐标为
的横坐标为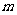 ;
;
①用含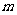 的代数式表示线段
的代数式表示线段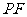 的长,并求出当
的长,并求出当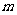 为何值时,四边形
为何值时,四边形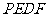 为平行四边形?
为平行四边形?
②设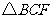 的面积为
的面积为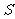 ,求
,求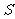 与
与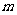 的函数关系式.
的函数关系式.
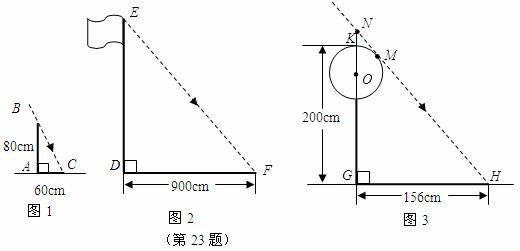
23.问题背景 在某次活动课中,甲、乙、丙三个学习小组于同一时刻在阳光下对校园中一些物体进行了测量.下面是他们通过测量得到的一些信息:
甲组:如图1,测得一根直立于平地,长为80cm的竹竿的影长为60cm.
乙组:如图2,测得学校旗杆的影长为900cm.
丙组:如图3,测得校园景灯(灯罩视为球体,灯杆为圆柱体,其粗细忽略不计)的高度为200cm,影长为156cm.
任务要求
(1)请根据甲、乙两组得到的信息计算出学校旗杆的高度;
(2)如图3,设太阳光线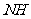 与⊙O相切于点
与⊙O相切于点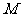 .请根据甲、丙两组得到的信息,求景灯灯罩的半径(友情提示:如图3,景灯的影长等于线段
.请根据甲、丙两组得到的信息,求景灯灯罩的半径(友情提示:如图3,景灯的影长等于线段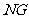 的影长;需要时可采用等式
的影长;需要时可采用等式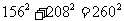 ).
).
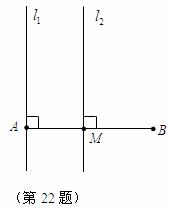
22.如图,已知线段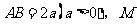 是
是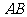 的中点,直线
的中点,直线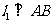 于点
于点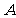 ,直线
,直线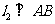 于点
于点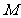 ,点
,点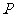 是
是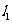 左侧一点,
左侧一点,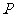 到
到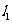 的距离为
的距离为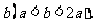
(1)作出点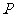 关于
关于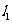 的对称点
的对称点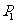 ,并在
,并在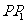 上取一点
上取一点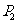 ,使点
,使点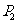 、
、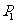 关于
关于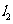 对称;
对称;
(2)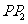 与
与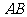 有何位置关系和数量关系?请说明理由.
有何位置关系和数量关系?请说明理由.
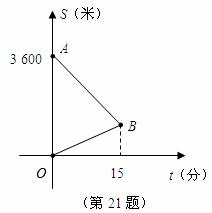
21.某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.下图中线段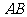 、
、 分别表示父、子俩送票、取票过程中,离体育馆的路程
分别表示父、子俩送票、取票过程中,离体育馆的路程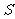 (米)与所用时间
(米)与所用时间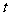 (分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(分钟)之间的函数关系,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)求点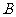 的坐标和
的坐标和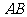 所在直线的函数关系式;
所在直线的函数关系式;
(2)小明能否在比赛开始前到达体育馆?
5.4 5.5 4.6 5.3 4.8 5.0 5.2 5.3 5.0 5.3
(1)若质量为(5±0.25)kg的为优等品,根据以上信息完成下表:
|
|
优等品数量(颗) |
平均数 |
方差 |
|
A |
|
4.990 |
0.103 |
|
B |
|
4.975 |
0.093 |
(2)请分别从优等品数量、平均数与方差三方面对A、B两种技术作出评价;从市场销售的角度看,你认为推广哪种种植技术较好.
5.0 4.8 5.2 4.9 5.2 5.0 4.8 5.2 5.1 5.0
B:4.5 4.9 4.8 4.5 5.2 5.1 5.0 4.5 4.7 4.9
20.经市场调查,某种优质西瓜质量为(5±0.25)kg的最为畅销.为了控制西瓜的质量,农科所采用A、B两种种植技术进行试验.现从这两种技术种植的西瓜中各随机抽取20颗,记录它们的质量如下(单位:kg):
A:4.1 4.8 5.4 4.9 4.7 5.0 4.9 4.8 5.8 5.2
19.某市今年中考理、化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试.小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(1)用“列表法”或“树状图法”表示所有可能出现的结果;
(2)小刚抽到物理实验B和化学实验F(记作事件M)的概率是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com