
24.(本题满分10分)
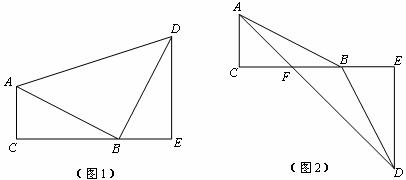
如图1,是美国总统Garfield于1876年给出的一种验证勾股定理的办法。Rt△ACB与Rt△DEB全等,点C、B、E共线,连接AD,可以证明△ABD是等腰三角形。如图2,Rt△ACB与Rt△DEB全等,点C、B、E共线,连接AD,交BC于点F,请你找出图2中的所有等腰直角三角形(不再添加线,不再添加字母),并给出证明。
23.(本题满分8分)
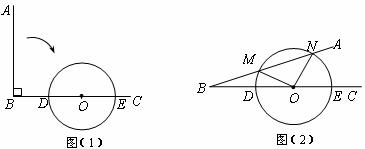
如图(1),∠ABC=90°,O为射线BC上一点,OB = 4,以点O为圆心,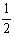 BO长为半径作⊙O交BC于点D、E。
BO长为半径作⊙O交BC于点D、E。
(1)当射线BA绕点B按顺时针方向旋转多少度时与⊙O相切?请说明理由.
(2)若射线BA绕点B按顺时针方向旋转与⊙O相交于M、N两点(如图(2)),MN=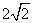 ,求的长.
,求的长.
22.(本题满分8分)
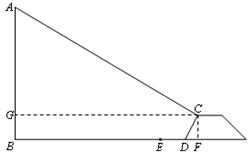
河岸边有一根电线杆AB(如下图),河岸距电线杆AB水平距离是14米,即BD=14米,该河岸的坡面CD的坡度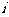 为
为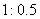 ,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(提示:在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域,
,岸高CF为2米,在坡顶C处测得杆顶A的仰角为30°,D、E之间是宽2米的人行道,请你通过计算说明在拆除电线杆AB时,为确保安全,是否将此人行道封上?(提示:在地面上以点B为圆心,以AB长为半径的圆形区域为危险区域,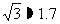 )
)
21.(本题满分8分)
某渔民准备承包一块正方形水域围网养鱼,通过调查得知:在该正方形水域四周的围网费用平均每千米0.25万元,上交承包费、购买鱼苗、饲料和鱼药等开支每平方千米需0.5万元。政府为鼓励渔民发展水产养殖,每位承包户补贴0.5万元.预计每平方千米养的鱼可售得4.5万元.若该渔民期望养鱼当年获得净收益3.5万元,你应建议该渔民承包多大面积的水域?
20.(本题满分8分)
已知二次函数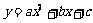 当
当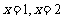 时,都有
时,都有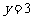 ,
,
当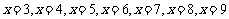 时,
时,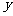 的值都是正整数,且
的值都是正整数,且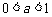 ,
,
求二次函数的解析式
19.(本题满分6分)
小王、小李和小林三人准备打乒乓球,他们约定用“抛硬币”的方式来确定哪两个人先上场,三人手中各持有一枚质地均匀的硬币,同时将手中硬币抛落到水平地面为一个回合。落地后,三枚硬币中,恰有两枚正面向上或者反面向上的两人先上场;若三枚硬币均为正面向上或反面向上,属于不能确定。
(1)请你完成下图中表示“抛硬币”一个回合所有可能出现的结果的树状图;
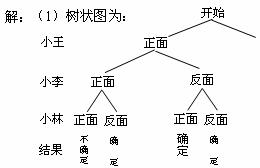
(2)求一个回合能确定两人先上场的概率.
18.(本题满分6分)
 ,并将其解集在数轴上表示出来.
,并将其解集在数轴上表示出来.
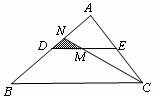
17.如图,DE是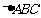 的中位线,M是DE的中点,CM的延长线交AB于N,那么
的中位线,M是DE的中点,CM的延长线交AB于N,那么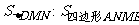 =_________________.
=_________________.
16.已知 是正整数,
是正整数, (
(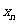 ,
,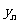 )是反比例函数
)是反比例函数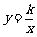 图象上的一列点,其中
图象上的一列点,其中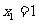 ,
,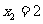 ,…,
,…,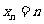 ;记
;记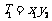 ,
,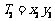 ,…,
,…,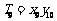 ;若
;若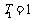 ,则
,则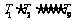 的值是______________.
的值是______________.
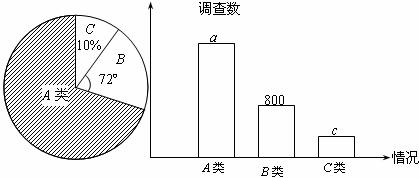
15.一项调查统计情况如图所示,本次抽样的样本容量是__________.图中c=_________.若被调查的对象占总体数的20%,请根据样本估计总体中A类对应的数值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com