
5.在数轴上,点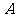 所表示的实数为3,点
所表示的实数为3,点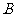 所表示的实数为
所表示的实数为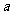 ,⊙A的半径为2。下列说法中不正确的是(
)
,⊙A的半径为2。下列说法中不正确的是(
)
A.当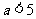 时,点
时,点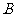 在⊙A内
在⊙A内
B.当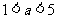 时,点
时,点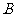 在⊙A内
在⊙A内
C.当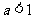 时,点
时,点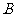 在⊙A外
在⊙A外
D.当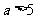 时,点
时,点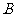 在⊙A外
在⊙A外
4.某中学篮球队12名队员的年龄情况如下:
|
年龄(单位:岁) |
14 |
15 |
16 |
17 |
18 |
|
人数 |
1 |
4 |
3 |
2 |
2 |
则这个队队员年龄的众数和中位数分别是( )
A.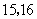 B.
B.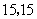 C.
C.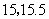 D.
D.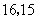
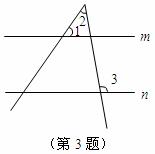
3.如图,直线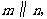
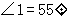
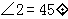 则
则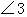 的度数为( )
的度数为( )
A.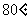 B.
B.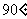 C.
C.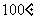 D.
D.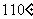
2.化简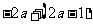 的结果是( )
的结果是( )
A. B.
B.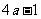 C.
C.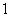 D.
D.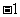
1.在0,-2,1,3这四数中,最小的数是( )
A.-2 B.0 C.1 D.3
27.课题研究(10分)(任选一题,若两题都选按得分最少的题记分,本题最高10分)
(1)甲乙两辆汽车在一条公路上匀速行驶,为了确定汽车的位置,我们用数轴O 表示这条公路,原点O为零千米路标(如图1),并作如下约定:
表示这条公路,原点O为零千米路标(如图1),并作如下约定:
①速度v>0,表示汽车向数轴正方向行驶;速度v<0,表示汽车向数轴负方向行驶;速度v=0,表示汽车静止.
②汽车位置在数轴上的坐标s>0,表示汽车位于零千米路标的右侧;汽车位置在数轴上的坐标s<0,表示汽车位于零千米路标的左侧;汽车位置在数轴上的坐标s=0,表示汽车恰好位于零千米路标处.
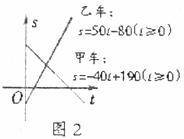
遵照上述约定,将这两辆汽车在公路上匀速行驶的情况,以一次函数图象的形式画在了同一直角坐标系中,如图2.
请解答下列问题:
①就这两个一次函数图像所反映的两汽车在这条公路上行驶的状况填写如下的表格.
|
|
行驶方向 |
速度的大小(km/h) |
出发前的位置 |
|
甲车 |
|
|
|
|
乙车 |
|
|
|
②甲乙两车能否相遇?如能相遇,求相遇时的时刻及在公路上的位置;如不能相遇,请说明理由.
(2)如图4表示一艘轮船与一艘快艇沿相同路线从甲港到乙港行驶过程中路程随时间变化的图象(分别是正比例函数图象和一次函数图象).
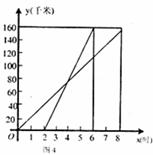
根据图象解答下列问题:
①请求出表示轮船、快艇行驶过程的函数解析式(不需写出自变量取值范围);
②快艇出发多长时间赶上轮船?
③轮船和快艇在途中(不包括起点和终点)行驶的速度分别是多少?
26.(本题10分)某一工程,在工程招标时,接到甲、乙两个工程队的投标熟,施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:
(1)甲队单独完成这项工程刚好如期完成;
(2)乙队单独完成这项工程要比规定日期多用6天;
(3)若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.
试问:在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
25.(10分)(任选一题,若两题都选按得分最少的题记分,本题最高10分)
(1)已知:如下图,反比例函数的图象经过点A、B,点A的坐标为(1,3).点B的纵坐标为1,点C的坐标为(2,0).
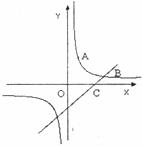
①求该反比例函数的解析式;
②求直线BC的解析式.
(2)己知一次函数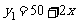 与
与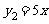 ,回答下列问题:
,回答下列问题:
①能否说函数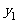 的值比函数
的值比函数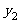 的值大?为什么?
的值大?为什么?
②这两个函数是否都随着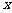 的增大而增大?
的增大而增大?
当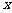 增加1个单位时,这两个函数的值分别增加多少?
增加1个单位时,这两个函数的值分别增加多少?
③当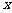 从1开始逐渐增大时,哪个函数的值先超过100?
从1开始逐渐增大时,哪个函数的值先超过100?
24.(8分)已知:如下图,△ABC是等边三角形,D为AC上任一点,∠ABD=∠ACE,BD=CE,求证:△ADE是等边三角形
23.(本题8分)如下图所示,已知△ABC,∠C=90°,AC=BC,按下列语句作图(尺规作图,保留痕迹,不必写作法)
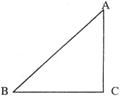
(1)作∠B的平分线,交AC于D ②过点D作DE⊥AB,垂足为E
(2)根据以上所作图形,写出四组相等的线段(不包括AC=BC)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com