
9.已知函数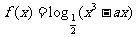 在区间
在区间 上为减函数,则实数
上为减函数,则实数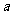 的取值范围为( )
的取值范围为( )
(A)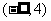 (B)
(B) (C)
(C)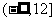 (D)
(D)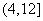
8.已知函数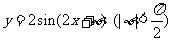 的图象经过点(0,1),则该函数图象的一条对称轴方程为 ( )
的图象经过点(0,1),则该函数图象的一条对称轴方程为 ( )
(A)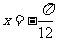 (B)
(B)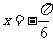 (C)
(C)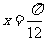 (D)
(D)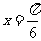
7.若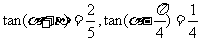 ,则
,则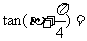 ( )
( )
(A)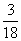 (B)
(B)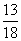 (C)
(C)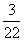 (D)
(D)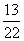
6.已知等差数列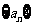 的前
的前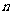 项和为
项和为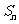 ,若
,若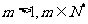 ,且
,且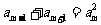 ,
,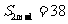 ,则m=( )
,则m=( )
(A)11 (B)10 (C)9 (D)8
5.已知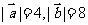 ,且
,且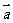 与2
与2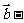
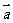 互相垂直,则
互相垂直,则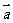 与
与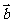 的夹角为( )
的夹角为( )
(A)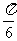 (B)
(B)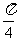 (C)
(C)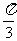 (D)
(D)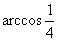
4.把函数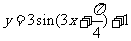 的图象按向量
的图象按向量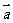 平移后,得到函数
平移后,得到函数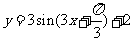 的图象,则向量
的图象,则向量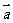 =( )
=( )
(A)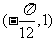 (B)
(B)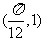 (C)
(C)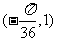 (D)
(D)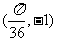
3.设函数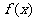 在
在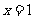 处连续,且
处连续,且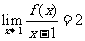 ,则
,则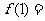 ( )
( )
(A)2 (B)1 (C)-1 (D)0
2.设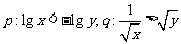 ,则p是q的 ( )
,则p是q的 ( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分又不必要条件
1.复数Z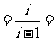 ( )
( )
(A)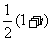 (B)
(B)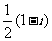 (C)
(C)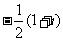 (D)
(D)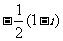
22.(理)(本题满分18分)
定义:若存在常数k,使得对定义域D内的任意两个不同的实数x1,x2,均有: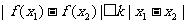 成立,则称
成立,则称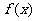 在D上满足利普希茨(Lipschitz)条件。
在D上满足利普希茨(Lipschitz)条件。
(1)试举出一个满足利普希茨(Lipschitz)条件的函数及常数k的值,并加以验证;
(2)若函数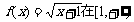 上满足利普希茨(Lipschitz)条件,求常数k的最小值;
上满足利普希茨(Lipschitz)条件,求常数k的最小值;
(3)现有函数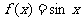 ,请找出所有的一次函数
,请找出所有的一次函数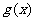 ,使得下列条件同时成立:
,使得下列条件同时成立:
①函数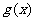 满足利普希茨(Lipschitz)条件;
满足利普希茨(Lipschitz)条件;
②方程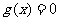 的根t也是方程
的根t也是方程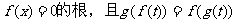 ;
;
③方程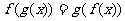 在区间
在区间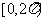 上有且仅有一解。
上有且仅有一解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com