
19.(本题满分16分)
已知命题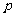 :
: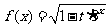 在
在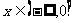 上有意义;命题
上有意义;命题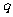 :数列
:数列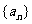 中
中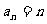 且对
且对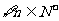 ,均有
,均有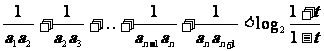 恒成立.若命题
恒成立.若命题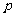 与
与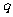 有且仅有一个是正确的,试求实数
有且仅有一个是正确的,试求实数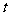 的取值范围.
的取值范围.
18.(本题满分16分)
已知椭圆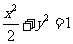 的左焦点为F,O为坐标原点。
的左焦点为F,O为坐标原点。
(I)求过点O.F,并且与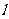 :
: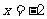 相切的圆的方程;
相切的圆的方程;
(II)设过点F且不与坐标轴垂直的直线交椭圆于A.B两点,线段AB的垂直平分线与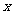 轴交于点G,求点G横坐标的取值范围
轴交于点G,求点G横坐标的取值范围
17.(本题满分14分)
统计表明,某种型号的汽车在匀速行驶中每小时的耗油量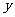 (升)关于行驶速度
(升)关于行驶速度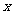 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: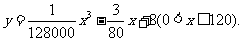 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。
(I)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
16.(本题满分14分)
在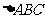 中,
中,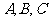 的对边分别为
的对边分别为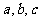 .
.
⑴若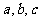 成等比数列,求
成等比数列,求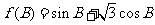 的值域;
的值域;
⑵若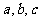 成等差数列,且
成等差数列,且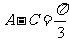 ,求
,求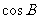 的值。
的值。
15.(本题满分14分)
已知直四棱柱ABCD-A1B1C1D1的底面是菱形,ÐB=60°, E, F分别是棱CC1与BB1上的点,且EC=BC=2FB,G为AE的中点。
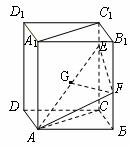
(1) 求证:GF∥平面ABCD;
(2)求证:平面AEF⊥平面AA1CC1。
14.设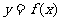 是定义在
是定义在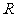 上的函数,给定下列三个条件:(1)
上的函数,给定下列三个条件:(1)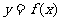 是偶函数;
是偶函数;
(2)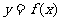 的图象关于直线
的图象关于直线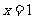 对称;
对称;
(3)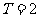 为
为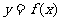 的一个周期.
的一个周期.
如果将上面(1)、(2)、(3)中的任意两个作为条件,余下一个作为结论,那么构成的三个命题中真命题的个数有 个.
二:解答题(共6大题,共计90分)
13.已知双曲线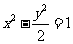 的焦点为F1、F2,点M在双曲线上且
的焦点为F1、F2,点M在双曲线上且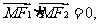 则点M
则点M
到x轴的距离为 .
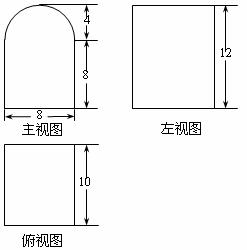
12.已知某个几何体的三视图如下(主视图的弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是 cm3.
11.关于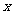 的方程
的方程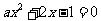 至少有一个正实根的充要条件是 。
至少有一个正实根的充要条件是 。
10.已知函数f (x) =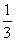 x3 +a x 2 +4 x存在极值,则实数a的取值范围是
。
x3 +a x 2 +4 x存在极值,则实数a的取值范围是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com