
19.(本小题满分16分)
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值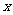 (单位:元,
(单位:元,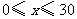 )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
(1)将一个星期的商品销售利润表示成 的函数;
的函数;
(2)如何定价才能使一个星期的商品销售利润最大?
18.(本小题满分14分)
设数列 的前
的前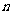 项和为
项和为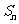 ,且
,且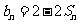 ;数列
;数列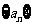 为等差数列,且
为等差数列,且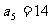 ,
,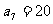 .(1)求数列
.(1)求数列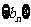 的通项公式;
的通项公式;
(2)若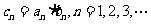 ,
,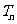 为数列
为数列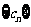 的前
的前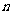 项和. 求证:
项和. 求证: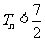 .
.
17.(本小题满分14分)
如图,在四棱锥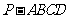 中,
中,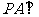 底面
底面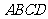 ,
,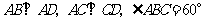 ,
,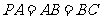 ,
,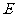 是
是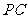 的中点.
的中点.
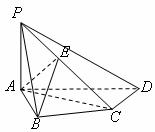
(1)证明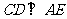 ;
;
(2)证明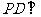 平面
平面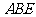 ;
;
16.(本小题满分14分)
在平面直角坐标系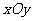 ,已知圆心在第二象限、半径为
,已知圆心在第二象限、半径为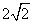 的圆
的圆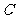 与直线
与直线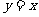 相切于坐标原点
相切于坐标原点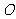 .椭圆
.椭圆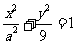 与圆
与圆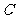 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为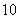 .
.
(1)求圆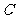 的方程;
的方程;
(2)试探究圆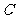 上是否存在异于原点的点
上是否存在异于原点的点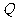 ,使
,使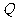 到椭圆右焦点
到椭圆右焦点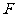 的距离等于线段
的距离等于线段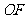 的长,若存在,请求出点
的长,若存在,请求出点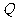 的坐标;若不存在,请说明理由
的坐标;若不存在,请说明理由
15.(本小题满分14分)
已知: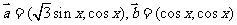 ,
,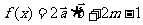 (
(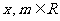 ).
).
(1) 求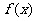 关于
关于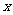 的表达式,并求
的表达式,并求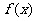 的最小正周期;
的最小正周期;
(2) 若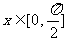 时
时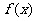 的最小值为5,求
的最小值为5,求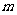 的值.
的值.
14.等差数列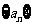 的前
的前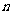 项和为
项和为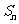 ,公差
,公差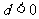 . 若存在正整数
. 若存在正整数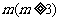 ,使得
,使得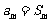 ,则当
,则当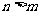 (
(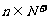 )时,有
)时,有 (填“>”、“<”、“=”).
(填“>”、“<”、“=”).
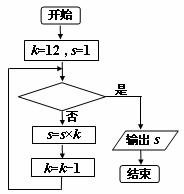
13.若框图所给的程序运行的结果为S=132,那么判断框中应填入的关于k的判断条件是 .
12.考察下列一组不等式:
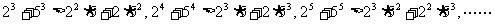 .
.
将上述不等式在左右两端仍为两项和的情况下加以推广,使以上的不等式成为推广不等式的特例,则推广的不等式可以是___________________.
11.设奇函数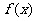 在
在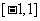 上是增函数,且
上是增函数,且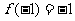 .若函数,
.若函数,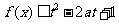 对所有的
对所有的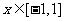 都成立,则当
都成立,则当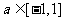 时,
时,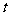 的取值范围是 .
的取值范围是 .
10.若抛物线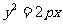 的焦点与椭圆
的焦点与椭圆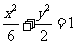 的右焦点重合,则
的右焦点重合,则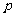 的值为 .
的值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com