
5.曲线在 在
在 处的切线的倾斜角为
( )
处的切线的倾斜角为
( )
A. B.
B. C.
C. D.
D.
4.设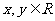 ,则“
,则“ ”是“
”是“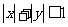 ”成立的
( )
”成立的
( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分也非必要条件
3.不等式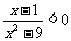 的解集为
( )
的解集为
( )
A.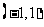 B.
B.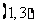 C.
C. D.
D.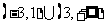
2.等比数列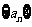 中,
中,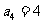 ,则
,则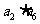 等于
( )
等于
( )
A. B.
B. C.
C.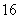 D.
D.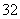
1.设全集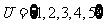 ,集合
,集合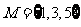 ,集合
,集合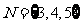 则集合
则集合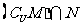 等于( )
等于( )
A.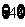 B.
B.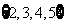 C.
C. D.
D.
20.(本小题共14分)
已知二次函数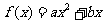 的图象过点
的图象过点 ,
, 是
是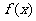 的导函数,且
的导函数,且
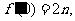
 .
.
(I)求a的值;
(II)若数列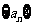 满足
满足 ,且
,且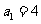 ,求数列
,求数列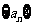 的通项公式;
的通项公式;
(III)对于(II)中的数列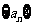 ,求证:
,求证: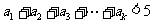
 .
.
19.(本小题共14分)
已知抛物线S的顶点在坐标原点,焦点在x轴上, 的三个顶点都在抛物线上,且
的三个顶点都在抛物线上,且 的重心为抛物线的焦点,若BC所在直线
的重心为抛物线的焦点,若BC所在直线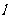 的方程为
的方程为
(I)求抛物线S的方程;
(II)若O是坐标原点,P,Q是抛物线S上的两动点,且满足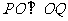 .试说明动直线PQ是否过定点.
.试说明动直线PQ是否过定点.
18.(本小题共12分)
某城市有30﹪的家庭订阅了A报,有60﹪的家庭订阅了B报,有20﹪的家庭同时订阅了A报和B报,从该城市中任取4个家庭.
(Ⅰ)求这4个家庭中恰好有3个家庭订阅了A报的概率;
(Ⅱ)求这4个家庭中至多有3个家庭订阅了B报的概率;
(Ⅲ)求这4个家庭中恰好有2个家庭A,B报都没有订阅的概率.
17.(本小题共14分)
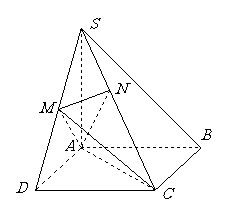
如图,在四棱锥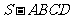 中,底面
中,底面 是正方形,
是正方形, 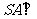 底面
底面 ,
,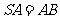 , 点
, 点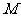 是
是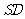 的中点,
的中点, ,且交
,且交 于点
于点 .
.
(I) 求证: 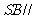 平面
平面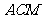 ;
;
(II)求二面角 的大小;
的大小;
(III)求证:平面 ⊥平面
⊥平面 .
.
16.(本小题共13分)
设数列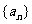 的前
的前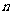 项和为
项和为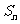 ,
,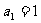 ,且数列
,且数列 是以2为公比的等比数列.
是以2为公比的等比数列.
(I)求数列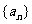 的通项公式;
的通项公式;
(II)求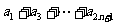 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com