A. 180    B. 160    C. 96    D. 60

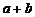解:取与取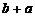是同一种取法.分类标准为两加数的奇偶性,第一类,偶偶相加,由分步计数原理得(10×9)/2=45种取法,第二类,奇奇相加,也有(10×9)/2=45种取法.根据分类计数原理共有45+45=90种不同取法.

例2 在1～20共20个整数中取两个数相加,使其和大于20的不同取法共有多少种?

解:分类标准一,固定小加数.小加数为1时,大加数只有20这1种取法;小加数为2时,大加数有19或20两种取法;小加数为3时,大加数为18,19或20共3种取法…小加数为10时,大加数为11,12,…,20共10种取法;小加数为11时,大加数有9种取法…小加数取19时,大加数有1种取法.由分类计数原理,得不同取法共有1+2+…+9+10+9+…+2+1=100种.

分类标准二:固定和的值.有和为21,22,…,39这几类,依次有取法10,9,9,8,8, …,2,2,1,1种.由分类计数原理得不同取法共有10+9+9+…+2+2+1+1=100种.

例3 如图一,要给①,②,③,④四块区域分别涂上五种颜色中的某一种,允许同一种颜色使用多次,但相邻区域必须涂不同颜色,则不同涂色方法种数为()

4．注意代换后参数的等价性

例8已知y＝2sinθcosθ＋sinθ－cosθ(0≤θ≤π)，求y的最大值、最小值

解：设t＝sinθ－cosθ＝sin(θ－)

∴2sinθcosθ＝1－ｔ²

∴y＝－ｔ²＋ｔ＋1＝－(ｔ－)²＋

又∵ｔ＝sin(θ－)，0≤θ≤π

教    学    过    程

组织教学          导入新课           讲授新课          归纳小结         布置作业

∴－≤θ－≤

∴－1≤ｔ≤

当ｔ＝时，y_max＝

当ｔ＝-1时，y_min＝－1

说明：此题在代换中，据θ范围，确定了参数ｔ∈［－1，］，从而正确求解，若忽视这一点，会发生ｔ＝时有最大值而无最小值的结论

五、课后作业：

六、板书设计（略）

七、课后记：

3．注意题中字母(参数)的讨论

例7求函数y＝sin²x＋acosx＋a－(0≤x≤)的最大值

解：∵y＝1－cos²x＋acosx＋a－＝－(cosx－)²＋＋a－

∴当0≤a≤2时，cosx＝，y_max＝＋a－

当a＞2时，cosx＝1，y_max＝a－

当a＜0时，cosx＝0，y_max＝a－

说明：解此题注意到参数a的变化情形，并就其变化讨论求解，否则认为cosx＝时，y有最大值会产生误解

4．用正弦函数和余弦函数的图象解最简单的三角不等式：通过例2介绍方法

例1 作下列函数的简图

(1)y=sinx，x∈[0，2π]，　　　 (2)y=cosx，x∈[0，2π]，

 (3)y=1+sinx，x∈[0，2π]，　 (4)y=-cosx，x∈[0，2π]，

解：(1)列表

X

0

Sinx

0

1

0

-1

0

(2)列表

X

0

Cosx

1

0

-1

0

1

(3)列表

X

0

Sinx

0

1

0

-1

0

1+sinx

1

2

1

0

1

(4)列表

X

0

Cosx

1

0

-1

0

1

 -cosx

-1

0

1

0

-1

教    学    过    程

组织教学          导入新课           讲授新课          归纳小结         布置作业

例2　利用正弦函数和余弦函数的图象，求满足下列条件的x的集合：

解：作出正弦函数y=sinx，x∈[0，2π]的图象：

由图形可以得到，满足条件的x的集合为：

解：作出余弦函数y=cos，x∈[0，2π]的图象：

由图形可以得到，满足条件的x的集合为：

五、小结  本节课我们学习了用单位圆中的正弦线、余弦线作正弦函数，余弦函数的图象，用五点法作正弦函数和余弦函数的简图，并用正弦函数和余弦函数的图象解最简单的三角不等式．

六、课后作业：

七、板书设计（略）

八、课后记：

教    学    过    程

组织教学          导入新课           讲授新课          归纳小结         布置作业

∴－≤sinx≤

∴当sinx＝－时

y_min＝－(－－)²＋＝

说明：解此题注意了条件｜x｜≤，使本题正确求解，否则认为sinx＝－1时y有最小值，产生误解

   3．用五点法作正弦函数和余弦函数的简图（描点法）：

正弦函数y=sinx，x∈[0，2π]的图象中，五个关键点是：

(0,0)  (,1)  (p,0)  (,-1)  (2p,0)

只要这五个点描出后，图象的形状就基本确定了．因此在精确度不太高时，

教    学    过    程

组织教学          导入新课           讲授新课          归纳小结         布置作业

常采用五点法作正弦函数和余弦函数的简图，要求熟练掌握．

探究：

（1）y=cosx,  xÎR与函数y=sin(x+)  xÎR的图象相同

（2）将y=sinx的图象向左平移即得y=cosx的图象

（3）也同样可用五点法作图：y=cosx   xÎ[0,2p]的五个点关键是

(0,1)  (,0)  (p,-1)  (,0)  (2p,1)

   2．用单位圆中的正弦线、余弦线作正弦函数、余弦函数的图象（几何法）：为了作三角函数的图象，三角函数的自变量要用弧度制来度量，使自变量与函数值都为实数．在一般情况下，两个坐标轴上所取的单位长度应该相同，否则所作曲线的形状各不相同，从而影响初学者对曲线形状的正确认识．

第一步：列表首先在单位圆中画出正弦线和余弦线．在直角坐标系的x轴上任取一点，以为圆心作单位圆，从这个圆与x轴的交点A起把圆分成

教    学    过    程

组织教学          导入新课           讲授新课          归纳小结         布置作业

几等份，过圆上的各分点作x轴的垂线，可以得到对应于角，，,…，2π的正弦线及余弦线（这等价于描点法中的列表）．

第二步：描点．我们把x轴上从0到2π这一段分成几等份，把角x的正弦线向右平行移动，使得正弦线的起点与x轴上相应的点x重合，则正弦线的终点就是正弦函数图象上的点．

第三步：连线用光滑曲线把这些正弦线的终点连结起来，就得到正弦函数y=sinx，x∈[0，2π]的图象．

现在来作余弦函数y=cosx，x∈[0，2π]的图象:

第一步:列表 表就是单位圆中的余弦线．

    第二步:描点．把坐标轴向下平移，过作与x轴的正半轴成角的直线，

又过余弦线A的终点A作x轴的垂线，它与前面所作的直线交于A′，那么A与AA′长度相等且方向同时为正，我们就把余弦线A“竖立”起来成为AA′，用同样的方法，将其它的余弦线也都“竖立”起来．再将它们平移，使起点与x轴上相应的点x重合，则终点就是余弦函数图象上的点．

第三步：连线．用光滑曲线把这些竖立起来的线段的终点连结起来，就得到余弦函数y=cosx，x∈[0，2π]的图象．

以上我们作出了y=sinx，x∈[0，2π]和y=cosx，x∈[0，2π]的图象，现在把上述图象沿着x轴向右和向左连续地平行移动，每次移动的距离为2π，就得到y=sinx，x∈R和y=cosx，x∈R的图象，分别叫做正弦曲线和余弦曲线．

1． 正弦线、余弦线：设任意角α的终边与单位圆相交于点P(x，y)，过P作x轴的垂线，垂足为M，则有

，

向线段MP叫做角α的正弦线，有向线段OM叫做角α的余弦线．

2．比值叫做的正弦    记作： 

 比值叫做的余弦    记作： 

 比值叫做的正切    记作： 

比值叫做的余切    记作： 

比值叫做的正割    记作： 

  比值叫做的余割    记作：   

以上六种函数，统称为三角函数

教    学    过    程

组织教学          导入新课           讲授新课          归纳小结         布置作业

今天我们要研究怎样作正弦函数、余弦函数的图象，作三角函数图象的方法一般有两种：(1)描点法；(2)几何法(利用三角函数线)．但描点法的各点的纵坐标都是查三角函数表得到的数值，不易描出对应点的精确位置，因此作出的图象不够准确．几何法则比较准确．

(2)若曲线C上总存在不同的两点关于直线对称，试确定m的取值范围．