
∵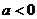 且
且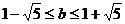 ,∴
,∴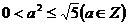 ,得
,得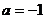 ,此时
,此时 或
或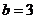 。
。
又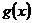 取最小值时,
取最小值时,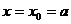 ,依题意,有
,依题意,有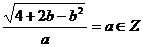 ,则
,则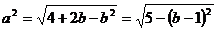 ,
,
此时,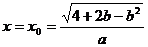 时,
时,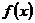 有最大值。
有最大值。
要使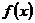 有最大值,必须满足
有最大值,必须满足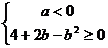 ,即
,即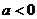 且
且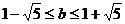 ,
,
(Ⅱ)若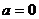 ,
,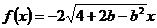 ,则
,则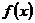 无最大值,故
无最大值,故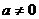 ,∴
,∴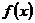 为二次函数,
为二次函数,
故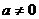 ,要使
,要使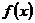 在
在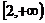 上单调递增,必须满足
上单调递增,必须满足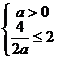 ,∴
,∴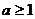 。
。
若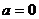 ,
,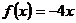 ,则
,则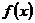 在
在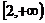 上单调递减,不符题意。
上单调递减,不符题意。
解:(Ⅰ)当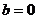 时,
时,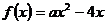 ,
,
(Ⅲ)对满足(Ⅱ)的条件的一个实数对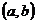 ,试构造一个定义在
,试构造一个定义在 ,且
,且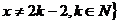 上的函数
上的函数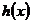 ,使当
,使当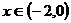 时,
时, ,当
,当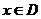 时,
时,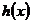 取得最大值的自变量的值构成以
取得最大值的自变量的值构成以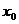 为首项的等差数列。
为首项的等差数列。
(Ⅱ)求满足下列条件的所有实数对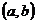 :当
:当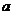 是整数时,存在
是整数时,存在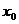 ,使得
,使得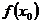 是
是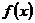 的最大值,
的最大值,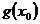 是
是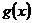 的最小值;
的最小值;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com