
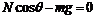 ②
②
24、解析:
据题意,小球P在球面上做水平的匀速圆周运动,该圆周的圆心为O’。P受到向下的重力mg、球面对它沿OP方向的支持力N和磁场的洛仑兹力
f=qvB ①
式中v为小球运动的速率。洛仑兹力f的方向指向O’。根据牛顿第二定律
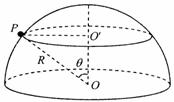 如图,一半径为R的光滑绝缘半球面开口向下,固定在水平面上。整个空间存在匀强磁场,磁感应强度方向竖直向下。一电荷量为q(q>0)、质量为m的小球P在球面上做水平的匀速圆周运动,圆心为O’。球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ<
如图,一半径为R的光滑绝缘半球面开口向下,固定在水平面上。整个空间存在匀强磁场,磁感应强度方向竖直向下。一电荷量为q(q>0)、质量为m的小球P在球面上做水平的匀速圆周运动,圆心为O’。球心O到该圆周上任一点的连线与竖直方向的夹角为θ(0<θ< 。为了使小球能够在该圆周上运动,求磁感应强度大小的最小值及小球P相应的速率。重力加速度为g。
。为了使小球能够在该圆周上运动,求磁感应强度大小的最小值及小球P相应的速率。重力加速度为g。
24.(19分)(2008年高考理综四川卷24题)
=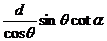
∴CM=dcotα
R′=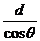
以上3式联立求解得
CM=dcotα
方法二:设圆心为A,过A做AB垂直NO,
可以证明NM=BO
∵NM=CMtanθ
又∵BO=ABcotα
=R′sinθcotα
 =
=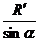
=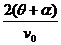
(3)
方法一:
CM=MNcotθ
t=T×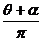
离子在磁场中做匀速圆周运动的周期T=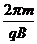
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com