
因为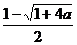 <0,
<0,  >
>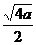 =
= ,所以,不等式②的解集为{x|
,所以,不等式②的解集为{x| <x<
<x< }.
}.
因为a>1,②式等价于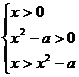
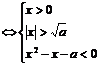

当n为奇数时, >0,不等式①等价于 logax>loga(x2-a).
②
>0,不等式①等价于 logax>loga(x2-a).
②
logax-4?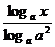 +12?
+12?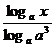 +…+n(-2)n-1 ?
+…+n(-2)n-1 ? =[1-2+4+…+(-2)n-1] logax =
=[1-2+4+…+(-2)n-1] logax =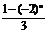 logax故原不等式可化为
logax故原不等式可化为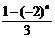 logax>
logax>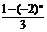 loga(x2-a). ①
loga(x2-a). ①
logax-log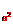 x+12log
x+12log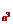 x+…+n (n-2)
x+…+n (n-2)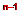 log
log x>
x>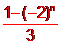 log
log (x2-a)
(x2-a)
解:利用对数换底公式,原不等式左端化为
即点B到平面EFG的距离为 .
.
【评析】该题作辅助线太多,难度过大,是历年立体几何题少见的难度;但它的出现,将中学教学的“距离”引向以点面距为核心的研究上,就当年而言,此题与考查双基的思想不符。
(1991年全国理科25题)已知n为自然数,实数a>1,解关于x的不等式
∴ OK= .
.
∴ 在Rt△HCG中,HG=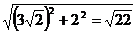 .
.
由于Rt△HKO和Rt△HCG有一个锐角是公共的,故Rt△HKO∽△HCG.
∴ AC=4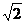 ,HO=
,HO=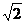 ,HC=3
,HC=3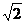 .
.
 ∵ BD⊥AC,
∵ BD⊥AC,
∴ EF⊥HC.
∵ GC⊥平面ABCD,
∴ EF⊥GC,
∴ EF⊥平面HCG.
∴ 平面EFG⊥平面HCG,HG是这两个垂直平面的交线. 作OK⊥HG交HG于点K,由两平面垂直的性质定理知OK⊥平面EFG,所以线段OK的长就是点B到平面EFG的距离.
∵ 正方形ABCD的边长为4,GC=2,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com