
(2006年浙江文理17)如图,在四棱锥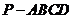 中,底面为直角梯形,
中,底面为直角梯形, ,
,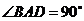 ,
, 底面
底面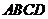 ,且
,且 ,
, 分别为
分别为 、
、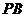 的中点。
的中点。
【评析】解至少有1,1.5,2,3,4,4.5,5七个,该题是一个错题,原答案为D。这是人们认识到“教师成长一靠专业化水平,二靠认真的态度”。
(2005年湖南理12)在(1+x)+(1+x)2+……+(1+x)6的展开式中,x 2项的系数是 .(用数字作答)
【解答】35
【评析】该题是一个老题,而且多数参考资料上有此原题,抄袭原题对于高考而言不是一件好事。
(2006年清华大学自主招生数学试题8)在所有定周长的空间四边形ABCD中,求对角线AC+BD的最大值,并证明
【评析】由于三角形ABD可以绕着对角线BD随意旋转,空间四边形的周长都不变,对角线AC没有最大值,故AC+BD也没有最大值。该题是一个错题。该题在国外引起的反响比较大,国内由于参加考试的人数比较少,没有形成大的影响。这使近年“教师的成长一在于自己的水平,二在于认真的态度,但更侧重于后者”的观点再次得到验证。
(2005年福建理12) 是定义在R上的以3为周期的奇函数,且
是定义在R上的以3为周期的奇函数,且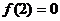 ,则方程
,则方程 在区间(0,6)内解的个数的最小值是
在区间(0,6)内解的个数的最小值是
A.2 B.
A.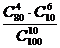 B.
B. C.
C.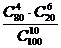 D.
D.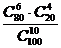 ”
”
【评析】该题又是重蹈历史覆辙的题目,类似有北京文8“五个工程队承建某项工程的五个不同的子项目,每个工程队承建1项,其中甲工程队不能承建1号子项目,则不同的承建方案共有(A) 种 (B)
种 (B)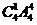 种 (C)
种 (C) 种 (D)
种 (D) 种”,辽宁3“设袋中有80个红球,20个白球,若从袋中任取10个球,则其中恰有6个红球的概率为( )
种”,辽宁3“设袋中有80个红球,20个白球,若从袋中任取10个球,则其中恰有6个红球的概率为( )
(A)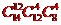 (B)
(B)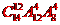 (C)
(C)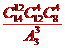 (D)
(D)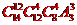
【解答】C
(A)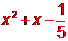 (B)
(B)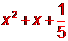 (C)
(C) (D)
(D)
【解答】B
【评析】该题一般的用逆推加数形结合方法选出,这样使从道理上说明的意图失落。
(2005年北京理7)北京《财富》全球论坛期间,某高校有14名志愿者参加接待工作.若每天排早、中、晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为
(2004年浙江理文12)若 和g(x)都是定义在实数集R上的函数,且方程
和g(x)都是定义在实数集R上的函数,且方程 有实数解,则
有实数解,则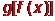 不可能是
不可能是
所以当a<0时,函数f(x)在区间(-∞,0)内为减函数,在区间(0,-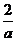 )内为增函数,在区间(-
)内为增函数,在区间(-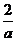 ,+∞)内为减函数.
,+∞)内为减函数.
由2x+ax2<0,解得x<0或x>-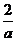 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com