第二个正六边形的周长

同理可得

∴OC=CD=

设C为AB的中点，连结OC，OB，则OC⊥AB

       A       B       

           C  E        

               D       

          O              

【评析】这些该题本身不难，但三角证明题几地都出现证法太多，标准不易统一，给阅卷带来非常大的难度。结论：三角证明一般不作为证明题出现。

   （1977年福建理科第3题）在半径为R的圆内接正六边形内，依次连结各边的中点，得一正六边形，又在这一正六边形内，再依次连结各边的中点，又得一正六边形，这样无限地继续下去，求：（1）前n个正六边形的周长之和S_n;（2）所有这些正六边形的周长之和S.

解：如图，半径为R的圆内接正六边形的周长为6R，

（1977年上海理科第1（4）题）求证：

=右边

证：左边=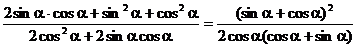

（1977年河北试题第3题）．证明：