
(2003年江苏20,辽宁22,天津理21文22)已知常数
 经过原点O以
经过原点O以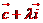 为方向向量的直线与经过定点
为方向向量的直线与经过定点 为方向向量的直线相交于P,其中
为方向向量的直线相交于P,其中
 试问:是否存在两个定点E、F,使得
试问:是否存在两个定点E、F,使得 为定值
为定值 若存在,求出E、F的坐标;若不存在,说明理由
若存在,求出E、F的坐标;若不存在,说明理由
则 ( ) (A)1 (B)
( ) (A)1 (B)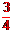 (C)
(C)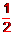 (D)
(D)
【解答】C
【评析】该题非常活,活得基本上学生思考不到,从而做不出。竞赛性质非常浓厚。引起人们对高考命题是该与竞赛题一样的“深挖洞”,还是“广积粮”的思考。
(2003年江苏9,全国7,天津理8)已知方程 的四个根组成一个首项为
的四个根组成一个首项为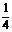 的的等差数列,
的的等差数列,
A.( ,1) B.
,1) B.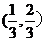 C.
C. D.
D.
则 的取值范围是 ( )
的取值范围是 ( )
【评析】该题需要多想多算,诸多能力聚于一题,突破了常规,单就题本身而言是一个好题,但突破常规的题一多,就显得整体试卷太过艰难。说白了,没有处理好研究与命题的关系。类似题有:(2003年辽宁11,全国理10文11,天津理10文11)已知长方形的四个顶点A(0,0),B(2,0),C(2,1)和D(0,1).一质点从AB的中点P0沿与AB夹角为θ的方向射到BC上的点P1后,依次反射到CD、DA和AB上的点P2,P3和P4(入射角等于反射角). 设P4的坐标为(x4,0),若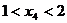 ,
,
(A)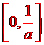 (B)
(B) (C)
(C)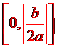 (D)
(D)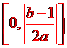
【解答】B
(2003年江苏8,辽宁9,天津理7)设 ,曲线
,曲线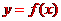 在点
在点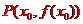 处切线的倾斜角的取值范围为
处切线的倾斜角的取值范围为 到曲线
到曲线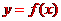 对称轴距离的取值范围为 ( )
对称轴距离的取值范围为 ( )
(2003年江苏5,天津理4文8)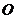 是平面上一定点,
是平面上一定点,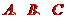 是平面上不共线的三个点,动点
是平面上不共线的三个点,动点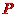 满足
满足 的轨迹一定通过
的轨迹一定通过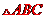 的
的
(A)外心 (B)内心 (C)重心 (D)垂心
【答案】B
【评析】当年《考试大纲》对于平面向量得基本定理是“了解”层次,当该题一致拔高到应用层次,属于把握不当出现的命题失误。
 (2003年江苏1)如果函数
(2003年江苏1)如果函数 的图象与
的图象与 轴有两个交点,则点
轴有两个交点,则点 平面上的区域(不包含边界)为(
)
平面上的区域(不包含边界)为(
)
【答案】C
【评析】该题不严格,关键在于a≠0对应图形中不应包含b轴;此题在当年争论非常大,甚至有一部分全国知名院士参予说“题出错”,搞得沸沸扬扬,甚至惊动国家领导人批示“妥善处理此”。现在看来,题出得不严格是个弱点,但对该题得选择不产生致命影响。通过该题产生了“教师成长的关键是什么?”的全国性大讨论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com