
6.如图所示,质量为m的球置于斜面上,被一个竖直挡板挡住。现用一个力F拉斜面,使斜面在水平面上做加速度为a的匀加速直线运动,忽略一切摩擦,以下说法中正确的是( )
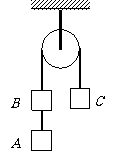
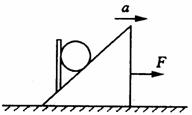
A.若加速度足够小,竖直挡板对球的弹力可能为零
B.若加速度足够大,斜面对球的弹力可能为零
C.斜面和挡板对球的弹力的合力等于ma
D.斜面对球的弹力不仅有,而且是一个定值
5.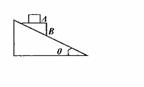 如图所示,A、B相对静止且一起沿倾角为θ的光滑斜面下滑,斜面体静止不动,则( )
如图所示,A、B相对静止且一起沿倾角为θ的光滑斜面下滑,斜面体静止不动,则( )
A.A受到弹力大小等于A的重力大小
B.A不受摩擦力
C.A受到水平向右的摩擦力
D.A受的摩擦力大小与sin2θ成反比
4.在粗糙的水平面上,一质量为m的物体在水平恒力T作用下做加速度为a的匀加速直线运动,如在物体上再加一个恒定的推力F,并保持其加速度不变,则所加的恒力F与水平面夹角的正切值为
A.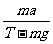 B.
B.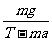 C.
C.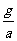 D.
D.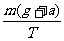
2.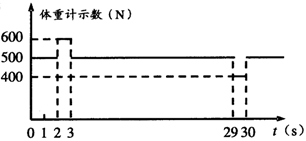 为了测量某住宅大楼每层的平均高度(层高)及电梯运行情况,甲、乙两位同学在一楼电梯内用电子体重计及秒表进行了以下实验:质量为m=50kg的甲同学站在体重计上,乙同学记录电梯从地面一楼到顶层全过程中,体重计示数随时间变化的情况,并作出了如图所示的图像。已知t=0时,电梯静止不动,从电梯内楼层按钮上获知该大楼共19层。取g
= l0m/s2 ,求:
为了测量某住宅大楼每层的平均高度(层高)及电梯运行情况,甲、乙两位同学在一楼电梯内用电子体重计及秒表进行了以下实验:质量为m=50kg的甲同学站在体重计上,乙同学记录电梯从地面一楼到顶层全过程中,体重计示数随时间变化的情况,并作出了如图所示的图像。已知t=0时,电梯静止不动,从电梯内楼层按钮上获知该大楼共19层。取g
= l0m/s2 ,求:
(1)电梯启动和制动时的加速度大小;
(2)该大楼的层高。
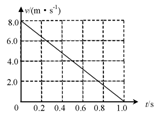 3.一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37º足够长的斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机做出了小物块上滑过程的速度-时间图线,如图所示。(取sin37º=0.6 cos37º=0.8 g
=10m/s2)求:
3.一质量m=2.0kg的小物块以一定的初速度冲上一倾角为37º足够长的斜面,某同学利用传感器测出了小物块冲上斜面过程中多个时刻的瞬时速度,并用计算机做出了小物块上滑过程的速度-时间图线,如图所示。(取sin37º=0.6 cos37º=0.8 g
=10m/s2)求:
(1)小物块冲上斜面过程中加速度的大小;
(2)小物块与斜面间的动摩擦因数;
1.两滑杆上分别套A、B两圆环,两环上分别用细线悬吊着两物体C、D,如图所示,当它们都沿滑杆向下滑动时,A的悬线始终与杆垂直,B的悬线始终竖直向下。则( )
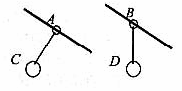 A. A环做的是匀速运动
A. A环做的是匀速运动
B. B环做的是匀速运动
C. A环与杆之间一定有摩擦力
D. B环与杆之间一定无摩擦力
10.(1)设滑块能与K个小球碰撞.整个过程中由动能定理得:-Kμmgs=0-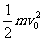 ,K=12.5,即能与12个小球碰撞.
,K=12.5,即能与12个小球碰撞.
(2)由动能定理得:-nμmgs=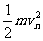 -
-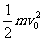 ①,滑块与小球碰撞后速度互换v=vn=
①,滑块与小球碰撞后速度互换v=vn=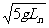 ②,由①②得碰撞中第n个小球的悬线长Ln=
②,由①②得碰撞中第n个小球的悬线长Ln=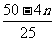 .
.
9.(1)当弹簧恢复原长时,B与C分离,0=mAvA-(mB+mc)vC①,EP=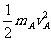 +
+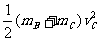 ②,对C由动能定理得W=
②,对C由动能定理得W=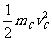 -0③,由①②③得W=18J,vA=vC=6m/s.
-0③,由①②③得W=18J,vA=vC=6m/s.
(2)取A、B为研究系统,mAvA -mB vC= mAvA’
+mB vC’, 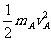 +
+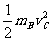 =
=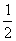 mAvA’
mAvA’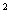 +
+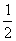 mB vC’
mB vC’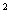 ,
,
当弹簧恢复到原长时A、B的速度分别为:,vA=vB=6m/s或vA=-2m/s, vB=10m/s.
8.取向右方向为正,m1v1-m2v2=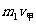 +
+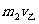 ,对乙由动能定理得W=
,对乙由动能定理得W=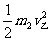 -
-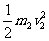 ,
,
当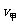 =
=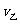 时,甲对乙做的功最少W=16.8J,当
时,甲对乙做的功最少W=16.8J,当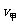 =-
=-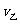 时,甲对乙做的功最多W=600J,
时,甲对乙做的功最多W=600J,
甲对乙做功的数值范围为16.8J≤W≤600J.
7.(1)设瞬时喷出m1的氧气,宇航员才能安全返回.0= m1v0-Mv①,返回时间t=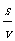 ②,呼吸消耗的氧气m2=Qt③,安全返回m1+m2≤m0④,由①②③④得0.05kg≤m≤0.45kg.
②,呼吸消耗的氧气m2=Qt③,安全返回m1+m2≤m0④,由①②③④得0.05kg≤m≤0.45kg.
(2)总耗氧量= m1+m2= m1+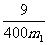 ,当m1=0.15kg时,总耗氧量最低,此时返回时间t=
,当m1=0.15kg时,总耗氧量最低,此时返回时间t=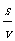 =600s.
=600s.
2.4动量和能量(二)(答案)
[例题]例1.(1)Mv0-mv0=(M+m)v,速度v=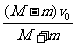 ①,方向水平向右.
①,方向水平向右.
(2)恰好没有滑离,则Q=fl0=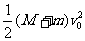 -
-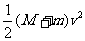 ②,A向左运动到达最远处时速度为0,
②,A向左运动到达最远处时速度为0,
对由动能定理得:-fs=0-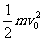 ③,由①②③得s=
③,由①②③得s=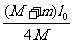 .
.
例2.(1)T=9.6N.(2)能.设第K次碰撞恰能完成完整的圆周运动,则vK=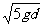 ①,整个过程中由动能定理得:-(2K-1)μmg
①,整个过程中由动能定理得:-(2K-1)μmg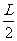 =
=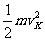 -
-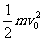 ②,由①②得小球能完成完整的圆周运动10次.
②,由①②得小球能完成完整的圆周运动10次.
例3. (1)设每个小球质量为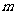 ,以
,以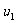 、
、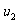 分别表示弹簧恢复到自然长度时左右两端小球的速度. 由动量守恒和能量守恒定律得
分别表示弹簧恢复到自然长度时左右两端小球的速度. 由动量守恒和能量守恒定律得 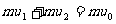 (以向右为速度正方向)
(以向右为速度正方向) 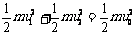 解得
解得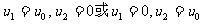
由于振子从初始状态到弹簧恢复到自然长度的过程中,弹簧一直是压缩状态,弹性力使左端小球持续减速,使右端小球持续加速,因此应该取解: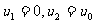
(2)以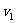 、
、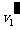 分别表示振子1解除锁定后弹簧恢复到自然长度时左右两小球的速度,规定向右为速度的正方向,由动量守恒和能量守恒定律,
分别表示振子1解除锁定后弹簧恢复到自然长度时左右两小球的速度,规定向右为速度的正方向,由动量守恒和能量守恒定律,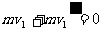
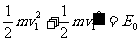 解得
解得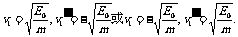
在这一过程中,弹簧一直是压缩状态,弹性力使左端小球向左加速,右端小球向右加速,故应取解: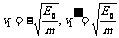 振子1与振子2碰撞后,由于交换速度,振子1右端小球速度变为0,左端小球速度仍为
振子1与振子2碰撞后,由于交换速度,振子1右端小球速度变为0,左端小球速度仍为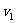 ,此后两小球都向左运动,当它们向左的速度相同时,弹簧被拉伸至最长,弹性势能最大,设此速度为
,此后两小球都向左运动,当它们向左的速度相同时,弹簧被拉伸至最长,弹性势能最大,设此速度为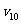 ,根据动量守恒定律:
,根据动量守恒定律: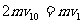
用E1表示最大弹性势能,由能量守恒有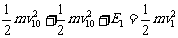
解得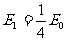 .
.
[练习]1.BD 2.CD 3.AB 4.C 5.B 6.C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com