
5.用脱脂棉包住约0.2g过氧化钠粉末,置于石棉网上,向脱脂棉上滴水,观察到脱脂棉剧烈燃烧起来。
(1)由上述实验现象所得到的有过氧化钠跟水反应的结论是:
第一,为氧气生成,
 第二,
。
第二,
。
Na2O2跟水反应的化学方程式是
。
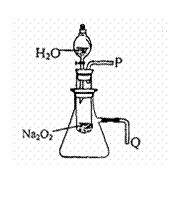
(2)某研究性学习小组拟用右图所示装置(气密
性良好)进行实验,以证明上述结论。
用以验证第一条结论的实验操作及现象是:
。
用以验证第二条结论的实验操作及现象是:
。
(3)实验(2)向试管中加水至固体完全溶解且不再有气泡生成后,取出度管,向试管中滴入酚酞试液,发现溶液先变红后退色,为探究其原因,该小组同学从查阅有关资料中得知:Na2O2与水反应可生成H2O2,H2O2具有强氮化性的漂白性。
请设计一个简单的实验,验证Na2O2跟足量水充分反应后的溶液中有H2O2存在。(只要求写出实验所用的试剂及观察到的现象)
试剂: ;
现象: 。
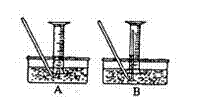 (4)该小组同学提出用定量的方法探究Na2O2跟水反应后的溶液中是否含有H2O2,其实验方法为:称取2.6gNa2O2固体,使之与足量的水反应,测量产生O2的体积并与理论值比较,即可得出结论:
(4)该小组同学提出用定量的方法探究Na2O2跟水反应后的溶液中是否含有H2O2,其实验方法为:称取2.6gNa2O2固体,使之与足量的水反应,测量产生O2的体积并与理论值比较,即可得出结论:
①测量气体体积时,必须持试管和量筒内的气体
都冷却至室温时进行,应选用如图装置中的
(忽略导管在量筒中所占的体积)
(填序),理由是
。
②若在标准状况下测量气体的体积,应选用的量
筒的大小规格为 (选填“100mL”、“200mL”、“500mL”或“1000mL”)
4. 一定温度下,向饱和NaOH溶液中投入一小块金属钠,充分反应后恢复到原来温度。下列叙述中,不合理的是
A.NaOH溶液浓度增大,并入出H2 B.溶液中NaOH的质量分数不变,有H2放出
C.总溶液的质量减小,有H2放出 D.钠浮于液面,到处游动,发出咝咝的响声
3. 背景材料:①2006年5月信息时报报道:世界卫生组织建议每天钠的摄取量少于2000mg,长期过量摄入钠可能引起高血压肾病胃病;②2007年7月,广西加大人工降雨作业强度,使夏季旱情得以缓解;③空气是人类生存所必需的重大资源改善空气质量称为“蓝天工程”;④2008年夏季奥运会将在我国举行,这次奥运会要突出“绿色奥运 科技奥运 人文奥运”的理念.
下列相应说法不正确的是
A.钠是活泼金属,常常保存在煤油中,人们每天可提取少于2000mg的金属钠
B.AgI和干冰都可用于人工降雨
C.加大石油 煤炭的开采速度,增加化石燃料的供应量不利于“蓝天工程”的建设
D.把环境保护作为奥运设施规划和建设的首要条件之一
2. 在一定条件下,使CO和O2的混合气体26g充分反应,所得混合物在常温下跟足量的Na2O2固体反应,结果固体增重14g,则原混合气体中O2和CO的质量比可能是
A.9:4 B.1:1 C.7:6 D.6:7
1. 某溶液含有①NO3- ②HCO3- ③SO32- ④CO32- ⑤SO42-等五种阴离子。向其中加入少量的Na2O2固体后,溶液中的离子浓度基本保持不变的是(忽略溶液体积的变化)
A.① B.①②④ C.①③⑤ D.①③④⑤
2.3 因为二次函数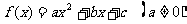 在区间
在区间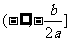 和区间
和区间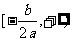 上分别单调,所以函数
上分别单调,所以函数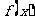 在闭区间上的最大值、最小值必在区间端点或顶点处取得;函数
在闭区间上的最大值、最小值必在区间端点或顶点处取得;函数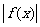 在闭区间上的最大值必在区间端点或顶点处取得.
在闭区间上的最大值必在区间端点或顶点处取得.
例7 已知二次函数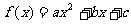 ,当
,当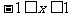 时,有
时,有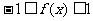 ,求证:当
,求证:当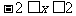 时,有
时,有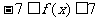 .
.
分析:研究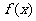 的性质,最好能够得出其解析式,从这个意义上说,应该尽量用已知条件来表达参数
的性质,最好能够得出其解析式,从这个意义上说,应该尽量用已知条件来表达参数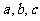 . 确定三个参数,只需三个独立条件,本题可以考虑
. 确定三个参数,只需三个独立条件,本题可以考虑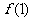 ,
,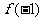 ,
,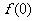 ,这样做的好处有两个:一是
,这样做的好处有两个:一是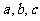 的表达较为简洁,二是由于
的表达较为简洁,二是由于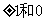 正好是所给条件的区间端点和中点,这样做能够较好地利用条件来达到控制二次函数范围的目的.
正好是所给条件的区间端点和中点,这样做能够较好地利用条件来达到控制二次函数范围的目的.
要考虑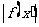 在区间
在区间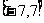 上函数值的取值范围,只需考虑其最大值,也即考虑
上函数值的取值范围,只需考虑其最大值,也即考虑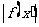 在区间端点和顶点处的函数值.
在区间端点和顶点处的函数值.
解:由题意知: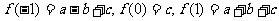 ,
,
∴ 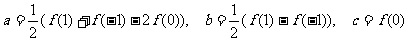 ,
,
∴ 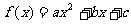
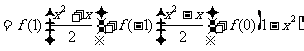 .
.
由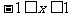 时,有
时,有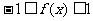 ,可得
,可得
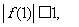
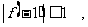
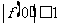 .
.
∴ 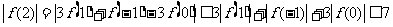 ,
,
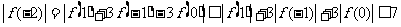 .
.
(1)若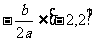 ,则
,则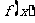 在
在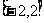 上单调,故当
上单调,故当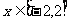 时,
时,
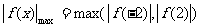
∴ 此时问题获证.
(2)若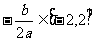 ,则当
,则当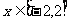 时,
时,
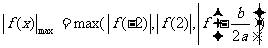
又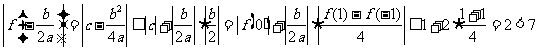 ,
,
∴ 此时问题获证.
综上可知:当 时,有
时,有 .
.
本资料由《七彩教育网》 提供!
本资料来源于《七彩教育网》
2.2 二次函数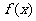 的图像具有连续性,且由于二次方程至多有两个实数根. 所以存在实数
的图像具有连续性,且由于二次方程至多有两个实数根. 所以存在实数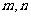 使得
使得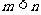 且
且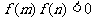
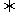 在区间
在区间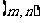 上,必存在
上,必存在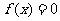 的唯一的实数根.
的唯一的实数根.
例6 已知二次函数 ,设方程
,设方程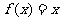 的两个实数根为
的两个实数根为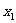 和
和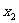 .
.
(1)如果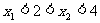 ,设函数
,设函数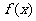 的对称轴为
的对称轴为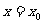 ,求证:
,求证: ;
;
(2)如果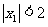 ,
,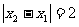 ,求
,求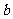 的取值范围.
的取值范围.
分析:条件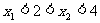 实际上给出了
实际上给出了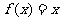 的两个实数根所在的区间,因此可以考虑利用上述图像特征去等价转化.
的两个实数根所在的区间,因此可以考虑利用上述图像特征去等价转化.
解:设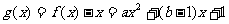 ,则
,则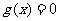 的二根为
的二根为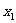 和
和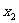 .
.
(1)由 及
及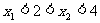 ,可得
,可得 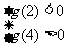 ,即
,即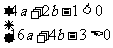 ,即
,即
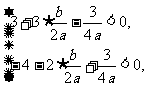
两式相加得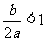 ,所以,
,所以, ;
;
(2)由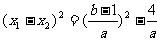 , 可得
, 可得
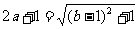 .
.
又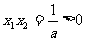 ,所以
,所以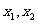 同号.
同号.
∴ 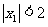 ,
,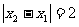 等价于
等价于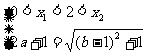 或
或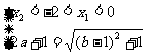 ,
,
即 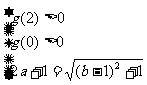 或
或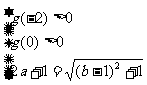
解之得 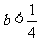 或
或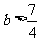 .
.
2.1 二次函数的图像关于直线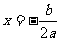 对称,
特别关系
对称,
特别关系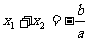 也反映了二次函数的一种对称性.
也反映了二次函数的一种对称性.
例5 设二次函数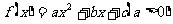 ,方程
,方程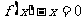 的两个根
的两个根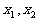 满足
满足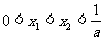 . 且函数
. 且函数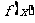 的图像关于直线
的图像关于直线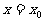 对称,证明:
对称,证明: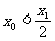 .
.
解:由题意
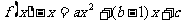 .
.
由方程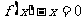 的两个根
的两个根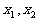 满足
满足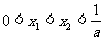 , 可得
, 可得
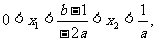 且
且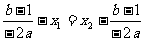 ,
,
∴  ,
,
即 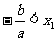 ,故
,故 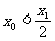 .
.
1.3 紧扣二次函数的顶点式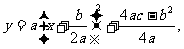 对称轴、最值、判别式显合力
对称轴、最值、判别式显合力
例4 已知函数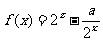 。
。
(1)将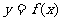 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数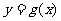 ,求函数
,求函数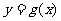 的解析式;
的解析式;
(2)函数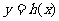 与函数
与函数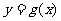 的图象关于直线
的图象关于直线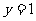 对称,求函数
对称,求函数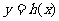 的解析式;
的解析式;
(3)设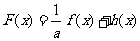 ,已知
,已知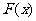 的最小值是
的最小值是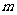 且
且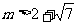 ,求实数
,求实数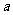 的取值范围。
的取值范围。
解:(1)
(2)设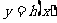 的图像上一点
的图像上一点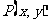 ,点
,点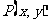 关于
关于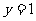 的对称点为
的对称点为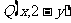 ,由点Q在
,由点Q在 的图像上,所以
的图像上,所以
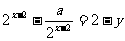 ,
,
于是 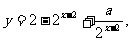
即 
(3)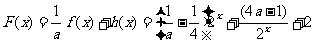 .
.
设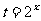 ,则
,则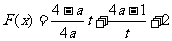 .
.
问题转化为: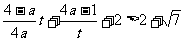 对
对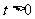 恒成立. 即
恒成立. 即
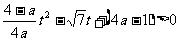 对
对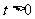 恒成立. (*)
恒成立. (*)
故必有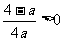 .(否则,若
.(否则,若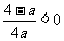 ,则关于
,则关于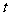 的二次函数
的二次函数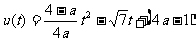 开口向下,当
开口向下,当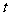 充分大时,必有
充分大时,必有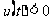 ;而当
;而当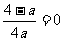 时,显然不能保证(*)成立.),此时,由于二次函数
时,显然不能保证(*)成立.),此时,由于二次函数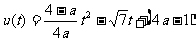 的对称轴
的对称轴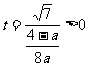 ,所以,问题等价于
,所以,问题等价于 ,即
,即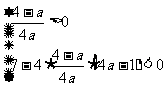 ,
,
解之得: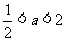 .
.
此时,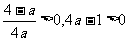 ,故
,故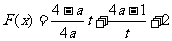 在
在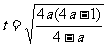 取得最小值
取得最小值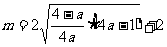 满足条件.
满足条件.
2 数形结合
二次函数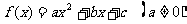 的图像为抛物线,具有许多优美的性质,如对称性、单调性、凹凸性等. 结合这些图像特征解决有关二次函数的问题,可以化难为易.,形象直观.
的图像为抛物线,具有许多优美的性质,如对称性、单调性、凹凸性等. 结合这些图像特征解决有关二次函数的问题,可以化难为易.,形象直观.
1.2 利用函数与方程根的关系,写出二次函数的零点式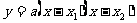
例3 设二次函数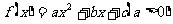 ,方程
,方程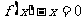 的两个根
的两个根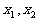 满足
满足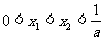 . 当
. 当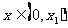 时,证明
时,证明 .
.
分析:在已知方程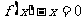 两根的情况下,根据函数与方程根的关系,可以写出函数
两根的情况下,根据函数与方程根的关系,可以写出函数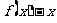 的表达式,从而得到函数
的表达式,从而得到函数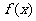 的表达式.
的表达式.
证明:由题意可知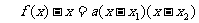 .
.
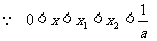 ,
,
∴ 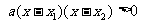 ,
,
∴ 当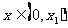 时,
时,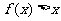 .
.
又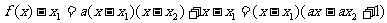 ,
,

∴ 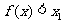 ,
,
综上可知,所给问题获证.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com