
3.疑点:抛物线的焦半径和焦点弦长公式.
(解决办法:引导学生证明并加以记忆.)
2.难点:抛物线的几何性质的应用.
(解决办法:通过几个典型例题的讲解,使学生掌握几何性质的应用.)
1.重点:抛物线的几何性质及初步运用.
(解决办法:引导学生类比椭圆、双曲线的几何性质得出.)
(三)学科渗透点
使学生进一步掌握利用方程研究曲线性质的基本方法,加深对直角坐标系中曲线方程的关系概念的理解,这样才能解决抛物线中的弦、最值等问题.
(二)能力训练点
从抛物线的标准方程出发,推导抛物线的性质,从而培养学生分析、归纳、推理等能力.
(一)知识教学点
使学生理解并掌握抛物线的几何性质,并能从抛物线的标准方程出发,推导这些性质.
22.(16分)
(Ⅰ)解(1)当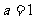 时,
时, 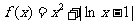
令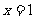 得
得 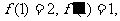 所以切点为(1,2),切线的斜率为1,
所以切点为(1,2),切线的斜率为1,
所以曲线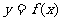 在
在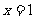 处的切线方程为:
处的切线方程为: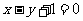 .
.
(Ⅱ)当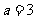 时
时
当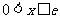 时,
时,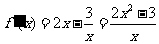 ,
,
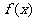 在
在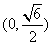 内单调递减,
内单调递减,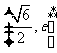 内单调递增;
内单调递增;
当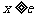 时,
时,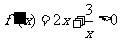 恒成立,故
恒成立,故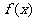 在
在 内单调递增;
内单调递增;
综上,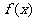 在
在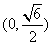 内单调递减,
内单调递减,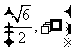 内单调递增.
内单调递增.
(Ⅲ)①当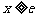 时,
时,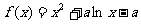 ,
,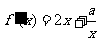
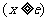
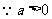 ,
,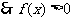 恒成立.
恒成立.
 在
在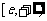 上增函数.
上增函数.
故当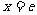 时,
时,
② 当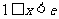 时,
时, ,
,
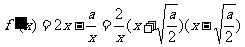 (
(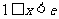 )
)
(i)当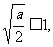 即
即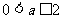 时,
时,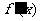 在
在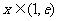 时为正数,所以
时为正数,所以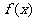 在区间
在区间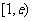 上为增函数.故当
上为增函数.故当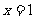 时,
时,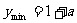 ,且此时
,且此时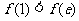
(ii)当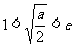 ,即
,即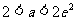 时,
时,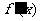 在
在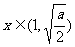 时为负数,在间
时为负数,在间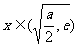 时为正数.所以
时为正数.所以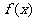 在区间
在区间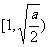 上为减函数,在
上为减函数,在 上为增函数
上为增函数
故当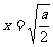 时,
时,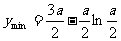 ,且此时
,且此时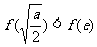
(iii)当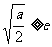 ;即
;即
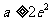 时,
时,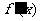 在
在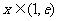 时为负数,所以
时为负数,所以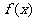 在区间[1,e]上为减函数,故当
在区间[1,e]上为减函数,故当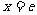 时,
时, .
.
综上所述,当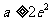 时,
时,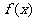 在
在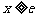 时和
时和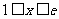 时的最小值都是
时的最小值都是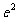 .
.
所以此时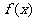 的最小值为
的最小值为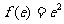 ;当
;当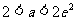 时,
时,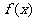 在
在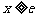 时的最小值为
时的最小值为
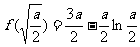 ,而
,而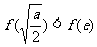 ,
,
所以此时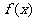 的最小值为
的最小值为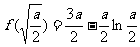 .
.
当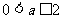 时,在
时,在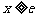 时最小值为
时最小值为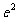 ,在
,在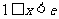 时的最小值为
时的最小值为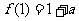 ,
,
而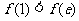 ,所以此时
,所以此时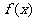 的最小值为
的最小值为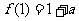
所以函数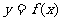 的最小值为
的最小值为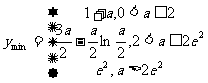
21.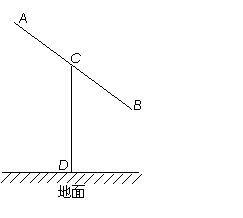 (14分)
(14分)
解:设 连结BD.
连结BD.
则在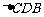 中,
中,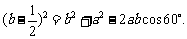

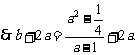
设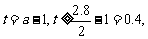
则
等号成立时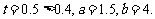
答:当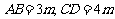 时,建造这个支架的成本最低.
时,建造这个支架的成本最低.
20.(14分)
(Ⅰ)∵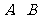 为锐角,
为锐角,
∴ 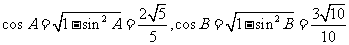
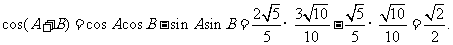
∵  ∴
∴ 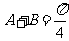
(II) 由(I)知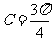 ,∴
,∴ 
由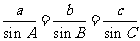 得
得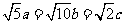 ,即
,即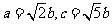
又∵ 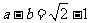 ∴
∴ 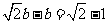 ∴
∴ 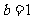 ∴
∴ 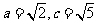
19.(14分)
(Ⅰ)函数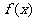 的定义域为R,且
的定义域为R,且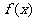 为奇函数,则有
为奇函数,则有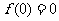
解得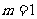
(II)任取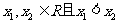 ,
,
则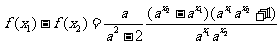 >0,又由
>0,又由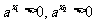 ,
,
可知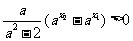
当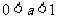 时,
时,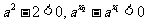 ,上式成立;
,上式成立;
当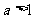 时,
时,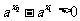 ,应有
,应有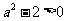 ,即
,即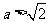 ,
,
综上, 的取值范围是
的取值范围是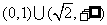
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com