
3、 能够根据30°、45°、60°角的三角函数值,说出相应的锐角的大小
教学重点和难点
重点:进行含有30°、45°、60°角的三角函数值的计算
难点:记住30°、45°、60°角的三角函数值
教学过程设计
一、 从学生原有的认知结构提出问题
上两节课,我们研究了正切、正弦、余弦函数,这节课,我们继续研究特殊角的三角函数值。
二、 师生共同研究形成概念
1、 引入
书本 P 10 引入
本节利用三角函数的定义求30°、45°、60°角的三角函数值,并利用这些值进行一些简单计算。
2、 30°、45°、60°角的三角函数值
通过与学生一起推导,让学生真正理解特殊角的三角函数值。


|
度数 |
sinα |
cosα |
tanα |
|
30° |
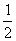 |
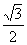 |
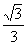 |
|
45° |
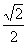 |
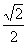 |
1 |
|
60° |
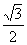 |
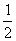 |
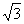 |
要求学生在理解的基础上记忆,切忌死记硬背。
3、 讲解例题
例1 计算:(1)sin30°+ cos45°; (2)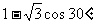 ;
;
(3)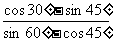 ; (4)
; (4)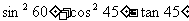 。
。
分析:本例是利用特殊角的三角函数值求解。
例2 填空:(1)已知∠A是锐角,且cosA = 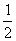 ,则∠A = °,sinA = ;
,则∠A = °,sinA = ;
(2)已知∠B是锐角,且2cosA = 1,则∠B = °;
(3)已知∠A是锐角,且3tanA 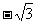 = 0,则∠A = °;
= 0,则∠A = °;
例3  一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角相同,求它摆至最高位置时与其摆至最低位置时的高度之差。
一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,且两边的摆动角相同,求它摆至最高位置时与其摆至最低位置时的高度之差。
分析:本例是利用特殊角的三角函数值求解的具体应用。
例4 在Rt△ABC中,∠C = 90°,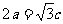 ,求
,求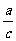 ,∠B、∠A。
,∠B、∠A。
分析:本例先求出比值后,利用特殊角的三角函数值,再确定角的大小。
三、 随堂练习
2、 能够进行含有30°、45°、60°角的三角函数值的计算
1、 经历探索30°、45°、60°角的三角函数值的过程,能够进行有关推理,进一步体会三角函数的意义
22.(本题满分14分)
设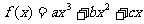 的极小值为-8,其导函数
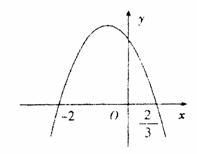
的极小值为-8,其导函数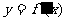 的图象经过点
的图象经过点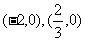 ,如图所示。
,如图所示。
(1)求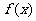 的解析式;
的解析式;
 (2)若对
(2)若对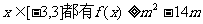 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
21.(本题满分12分)
已知函数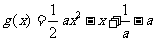 ,且
,且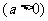 .
.
(1)求函数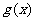 在
在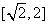 上的最小值
上的最小值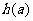 ;
;
(2)求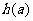 的值域。
的值域。
20.(本题满分12分)
已知函数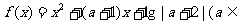 R,且
R,且 .
.
(I)若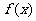 能表示成一个奇函数
能表示成一个奇函数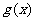 和一个偶函数
和一个偶函数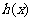 的和,求
的和,求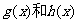 的解析
的解析
式;
(II)命题P:函数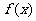 在区间
在区间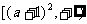 上是增函数;
上是增函数;
命题Q:函数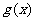 是减函数.
是减函数.
如果命题P、Q有且仅有一个是真命题,求a的取值范围;
(III)在(II)的条件下,比较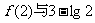 的大小.
的大小.
19.(本题满分12分)
已知函数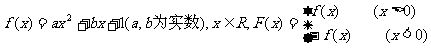
(1)若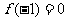 且函数
且函数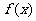 的值域为
的值域为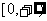 ,求
,求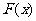 的表达式;
的表达式;
(2)设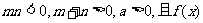 为偶函数,判断
为偶函数,判断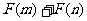 能否大于零?并说明理由。
能否大于零?并说明理由。
18.(本题满分12分)
已知函数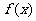 的定义域是
的定义域是 ,当
,当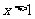 时,
时,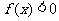 ,且
,且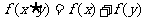 .
.
(Ⅰ)证明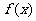 在定义域上是减函数;
在定义域上是减函数;
(Ⅱ)如果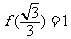 ,求满足不等式
,求满足不等式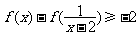 的
的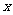 的取值范围.
的取值范围.
17.(本题满分12分)
记函数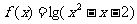 的定义域为集合A,函数
的定义域为集合A,函数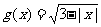 的定义域为集合B.
的定义域为集合B.
(1)求A∩B和A∪B;
(2)若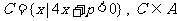 ,求实数
,求实数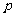 的取值范围.
的取值范围.
15.已知集合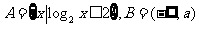 ,若
,若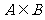 则实数
则实数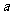 的取值范围是
的取值范围是 ,其中
,其中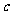 = .
16.已知
= .
16.已知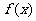 是
是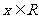 上的偶函数,
上的偶函数,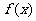 的图像向右平移一个单位长度又得到一个奇函数,且
的图像向右平移一个单位长度又得到一个奇函数,且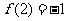 ;则
;则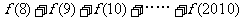 =
=
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com