10．

⑴对月球 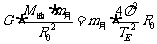　　 对卫星

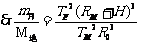
⑵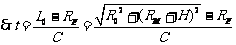

9．

解：(1)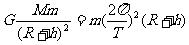

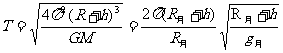
　　　 (2)

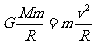
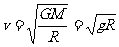
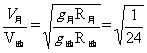
8、

(1)假设地球质量为M　 有g=GM/R²(2分)

　设月球绕地球运动的轨道半径为r　 有GMm_月/r²=m_月r(2/T)²(2分)

由上面可知：r=³√gT²R²/4²(3分)

　 (2)设下落到月面的时间为t　 有h=g_月t²/2　　　　　 　　　　　　　　　(2分)

S=V₀t　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　　(2分)

可得：g_月=2hv₀²/S² 　　　　　　　　　　　　　　　　　　　　　　　(1分)

有g_月=GM_月/R_月² 　　　　　　　　　　　　　　　　　　　　　　　　　(2分)

M月=2hR_月²v₀²/GS² 　　　　　　　　　　　　　　　　　　　　　　　　(2分)

7．

解：⑴设月球的质量为M，飞船的质量为m，则

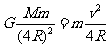　　　　　　　　　　　　　　　　　　　 (2分)

　　　　　　　　　　　　　　　　　　　　　 (2分)

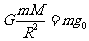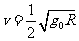解得 　　　　　　　　　　　　　　　　　　　 (2分)

⑵动能减小　　　　　　　　　　　　　　　　　　　　　　 (2分)

⑶设飞船在轨道Ⅲ绕月球运行一周所需的时间为T，则

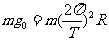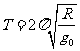　　　　　　　　　　　　　　　　　　　 (2分)

∴　　　　　　　　　　　　　　　　　　　　 (2分)

6．

(1)机器人在月球上用弹簧秤竖直悬挂物体，静止时读出弹簧秤的读数F，即为物体在月球上所受重力的大小　 (2分)

(2)在月球上忽略月球的自转可知　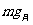 =F　 ①(2分)　 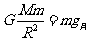　② (2分)

飞船在绕月球运行时，因为是靠近月球表面，故近似认为其轨道半径为月球的半径R，由万有引力提供物体做圆周运动的向心力可知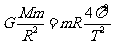③(2分)

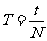又 ④(2分)

由①．②．③．④式可知月球的半径 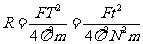　(2分)

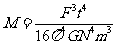月球的质量　 　　　　　　(2分)

5．

　解析：：⑴设中央恒星O的质量为M，A行星的质量为m，则由万有引力定律和牛顿第二定律得　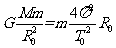 　　(3分)解得　 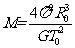　　(2分)

⑵由题意可知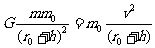： (3分) 　(2分)

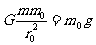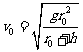解得 (2分)

4、

(1)探月飞船作圆周运动所需的向心力由月球对探月飞船的万有引力提供有　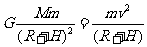　 　……………(1) (3分)

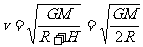　……………(2) (2分)

(2)不正确 ；　 因探月飞船从月球表面发送到H高处的过程中月球的引力为变力，故克服引力所做的功不等于mgH．　 ……………(3)(2分)

由引力势能定义可知探月飞船从月球表面发送到H处引力势能的改变量

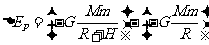　……………(4)(2分)

整理后得　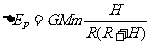 ……………(5)(2分)

由能量守恒定律可知，将探月飞船从月球表面发送到H处所需的能量为

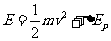　………(6)(2分)

联立求解得　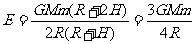 ……………(7)(2分)

3.

解析：(1)由星体均围绕正方形对角线的交点做匀速圆周运动可知，星体做匀速圆周运动的轨道半径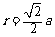　　 (3分)

(2)由万有引力的定律可知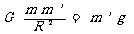　 (3分)

则星体表面的重力加速度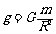　　 (3分)

(3)星体在其他三个星体的万有引力作用下围绕正方形对角线的交点做匀速圆周运动，由万有引力定律和向心力公式得：

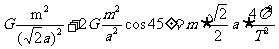　 (3分)

解得周期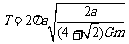　 　　　　(3分)

2、

解：(1)飞船在圆轨道上做匀速圆周运动，飞船受到地球的万有引力提供了飞船的向心力，设飞船绕地球运行的加速度大小为a，根据万有引力定律和牛顿第二定律，有

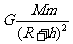＝ma　　　　　　　　　　　　　　　　　　　　　　　　　　　 (2分)

物体在地球表面上受到的万有引力近似等于物体受到的重力，即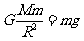　 (1分)

解得 a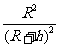＝g　　 　　　　　　　　　　　　　　　　　　　　　　　(2分)

(2)设飞船绕地球运行的周期为T，根据万有引力定律和牛顿第二定律，有

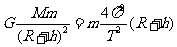　　　　　　　　　　　　　　　　 　　　　　　(2分)

物体在地球表面上受到的万有引力近似等于物体受到的重力，即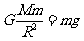　 (1分)

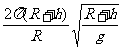解得 T＝ 　　　　　　　　　　　　　　　　　　　　　　　(2分)

1、

解：(1)机器人在月球上用弹簧秤竖直悬挂物体，静止时读出弹簧秤的读数F，即为物体在月球上所受重力的大小　 (5分)

(2)在月球上忽略月球的自转可知　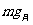 =F　 ①　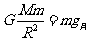 　②　 (2分)

飞船在绕月球运行时，因为是靠近月球表面，故近似认为其轨道半径为月球的半径R，由万有引力提供物体做圆周运动的向心力可知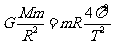③(2分)又 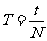④(2分)

由①、②、③、④式可知月球的半径　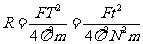 　　(2分)

月球的质量　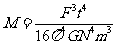 　　　　　　(2分)