
2.当图中α的角度由最大逐渐变小时
A.太阳直射点由南回归线向北移动 B.北极圈内的极昼范围逐渐缩小
C.太阳直射点由北回归线向南移动 D.南极圈内的极夜范围逐渐缩小
1.图中α的最大值可达
A.90° B.66°34′ C.30° D.23°26′
22、已知函数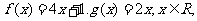 数列
数列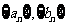 满足条件:
满足条件:
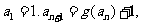
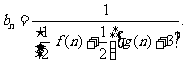
⑴求数列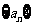 的通项公式;
的通项公式;
⑵求数列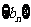 的前
的前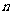 项和
项和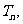 并求使得
并求使得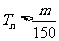 对任意
对任意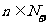 都成立的最大正整数
都成立的最大正整数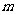 ;
;
⑶求证: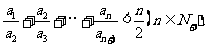




21、已知动圆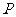 过点
过点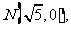 并且与圆
并且与圆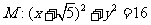 相外切
相外切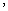 动圆圆心
动圆圆心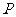 的轨迹为
的轨迹为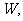 轨迹
轨迹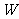 与
与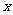 轴的交点为
轴的交点为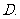
⑴求轨迹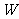 的方程;
的方程;
⑵设直线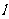 过点
过点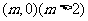 且与轨迹
且与轨迹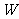 有两个不同的交点
有两个不同的交点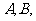 求直线
求直线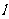 的斜率
的斜率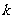 的取值范围;
的取值范围;
⑶在⑵的条件下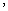 若
若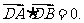 证明直线
证明直线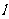 过定点
过定点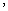 并求出这个定点的坐标
并求出这个定点的坐标
20、已知函数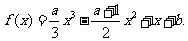
⑴若曲线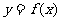 在点
在点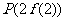 处的切线方程为
处的切线方程为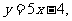 求函数
求函数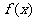 的解析式;
的解析式;
⑵当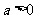 时
时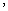 讨论函数
讨论函数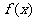 的单调性
的单调性
19、一个口袋装有编号分别为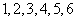 的小球各两个
的小球各两个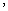 从中任取
从中任取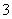 个球
个球
⑴求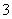 个球中最大编号为
个球中最大编号为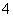 的概率; ⑵求
的概率; ⑵求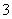 个球编号和恰能被
个球编号和恰能被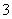 整除的概率
整除的概率
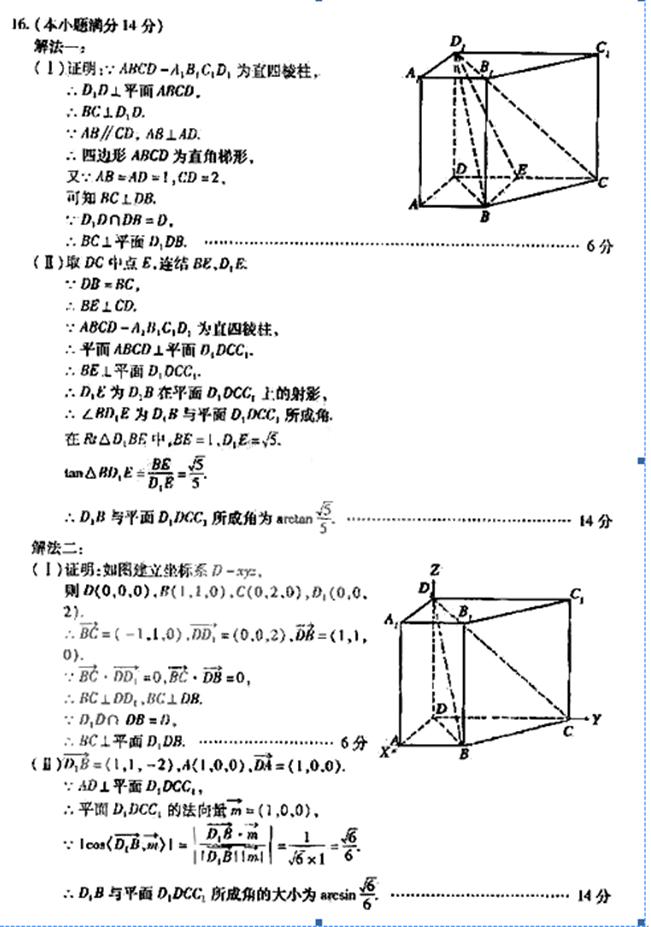
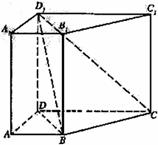
18、直四棱柱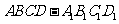 中
中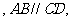
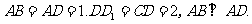
⑴求证: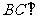 平面
平面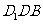 ; ⑵求
; ⑵求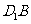 与平面
与平面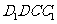 所成角的大小
所成角的大小
17、在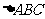 中,角
中,角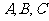 所对的边分别为
所对的边分别为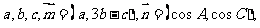 且
且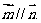
⑴求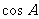 的值;
⑵求
的值;
⑵求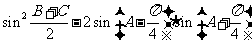 的值
的值
16、对于集合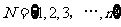 的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减,加后继的数,例如集合
的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减,加后继的数,例如集合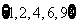 的交替和是
的交替和是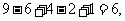 集合
集合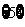 的交替和为
的交替和为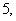 当集合
当集合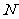 中的
中的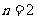 时
时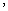 集合
集合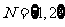 的所有非空子集为
的所有非空子集为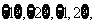 则它的“交替和”的总和
则它的“交替和”的总和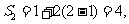 则当时
则当时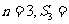 ,根据
,根据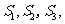 猜想集合
猜想集合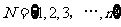 的每一个非空子集的“交替和”的总和
的每一个非空子集的“交替和”的总和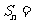 __________
__________
15、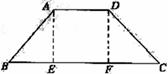 如图,等腰梯形
如图,等腰梯形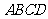 中,
中,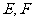 是
是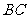 边上的两个三等分点,
边上的两个三等分点,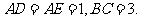 若三角形
若三角形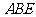 和
和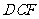 分别沿
分别沿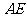 和
和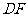 折起,使得
折起,使得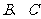 两点重合于一点
两点重合于一点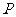 ,则二面角
,则二面角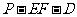 的大小为_________
的大小为_________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com