
4. 有三个人,每个人都以相同的概率被分配到四个房间中的每一间.试求(1)三个人都分配到同一房间的概率;(2)至少有两个人分配到同一房间的概率.
解:(1)三个人分配到同一房间有4种分法,故由等可能事件的概率可知,所求的概率为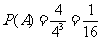 .
.
(2)设事件B为”至少有两人分配到同一房间”,则考虑事件B的剩余情况为”三个人分配到三个不同的房间”.∵三个人分配到三个不同房间共有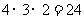 种方法,
种方法,
∴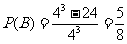 .
.
3. 正六边形的顶点共有6个,以其中2个点为端点连成的线段中,正好是正六边形的边的概率为____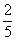 ________.
________.
2. 先后抛掷两颗骰子,设出现的点数之和是10,8,6的概率依次是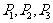 ,则(C )
,则(C )
A.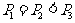 B.
B.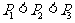
C.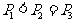 D.
D.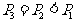
1. ①已经发生的事件一定是必然事件;
②随机事件的发生能够人为控制其发生或不发生;
③不可能事件反映的是确定性现象;
④随机现象的结果是可以预知的.
以上说法正确的是 (C )
A. ①③ B.①② C.③ D.②④
3. 有4条线段,长度分别为1,3,5,7,从这四条线段中任取三条,则所取三条线段能构成一个三角形的概率是___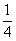 ________.
________.
[精典范例]
例1 事件”某人掷骰子5次,两次点数为2”是随机事件吗?条件和结果是什么?一次试验是指什么?一共做了几次试验?
解:是随机事件.条件:某人掷骰子5次,结果:两次点数为2,掷骰子一次就是一次试验,一共做了5次试验.
例2 从甲、乙、丙、丁四个人中选两名代表,求:
(1)甲被选中的概率;(2)丁没被选中的概率.
解:从甲、乙、丙、丁四个人中选两名代表包含6个基本事件: 甲乙、甲丙、甲丁、乙丙、乙丁、丙丁.
(1)记甲被选中为事件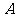 ,则
,则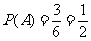 ;
;
(2)记丁没被选中为事件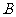 ,则
,则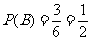 .
.
例3 袋中有大小相同的红、黄两种颜色的球各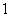 个,从中任取
个,从中任取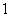 只,有放回地抽取
只,有放回地抽取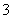 次. 求:
次. 求:
①
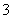 只全是红球的概率;
只全是红球的概率;
②
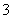 只颜色全相同的概率;
只颜色全相同的概率;
③ 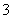 只颜色不全相同的概率.
只颜色不全相同的概率.
解:①每次抽到红球的概率为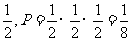
②每次抽到红球或黄球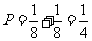
③颜色不全相同是全相同的对立,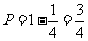
例4 现有一批产品共有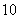 件,其中
件,其中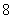 件为正品,
件为正品,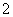 件为次品:
件为次品:
(1)如果从中取出一件,然后放回,再取一件,求连续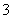 次取出的都是正品的概率;
次取出的都是正品的概率;
(2)如果从中一次取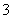 件,求
件,求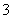 件都是正品的概率.
件都是正品的概率.
解:1)有放回地抽取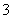 次,按抽取顺序
次,按抽取顺序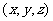 记录结果,则
记录结果,则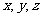 都有
都有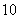 种可能,所以试验结果有
种可能,所以试验结果有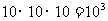 种;设事件
种;设事件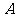 为“连续
为“连续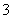 次都取正品”,则包含的基本事件共有
次都取正品”,则包含的基本事件共有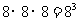 种,因此,
种,因此,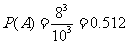
(2)可以看作不放回抽样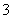 次,顺序不同,基本事件不同,按抽取顺序记录
次,顺序不同,基本事件不同,按抽取顺序记录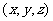 ,则
,则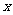 有
有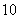 种可能,
种可能,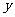 有
有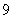 种可能,
种可能,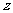 有
有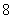 种可能,所以试验的所有结果为
种可能,所以试验的所有结果为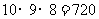 种
种 设事件
设事件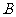 为“
为“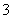 件都是正品”,则事件
件都是正品”,则事件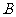 包含的基本事件总数为
包含的基本事件总数为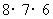 , 所以
, 所以 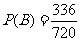
追踪训练
2. 在12件同类产品中,有10件是正品,2件是次品,从中任意抽出3件的必然事件是( D )
A.3件都是正品 B.至少有1件是次品
C.3件都是次品 D.至少有一件是正品
1. 下列事件中不可能事件是( C )
A.三角形的内角和为180°
B.三角形中大边对的角大,小边对的角小
C.锐角三角形中两个内角的和小于90°
D.三角形中任意两边的和大于第三边
2.复习古典概型及其概率公式,并进行综合应用.
[课堂互动]
自学评价
1.复习随机事件及其概率
4、已知集合
A=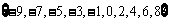 ,在平面直角坐标系中,点M的坐标为
,在平面直角坐标系中,点M的坐标为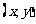 ,其中
,其中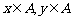 ,且
,且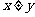 ,计算:(1)点M不在
,计算:(1)点M不在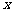 轴上的概率;(2)点M在第二象限的概率.
轴上的概率;(2)点M在第二象限的概率.
解:(1)满足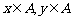 ,
,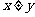 的点M的个数有10
的点M的个数有10 9=90,不在
9=90,不在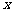 轴上的点的个数为9
轴上的点的个数为9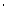 9=81个,∴点M不在
9=81个,∴点M不在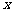 轴上的概率为:
轴上的概率为: 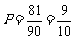 ;
;
(2)点M在第二象限的个数有5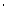 4=20个,所以要求的概率为
4=20个,所以要求的概率为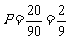 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com