
3、如果一个随机试验满足:
(1)试验中所有可能出现的基本事件只有有限个;
(2)每个基本事件的发生都是等可能的;
那么,我们称这个随机试验的概率模型为古典概型.
2、等可能基本事件:若在一次试验中,每个基本事件发生的可能性都相同,则称这些基本事件为等可能基本事件。
1、基本事件: 一次试验连同其中可能出现的每一个结果称为一个基本事件.
2、会用枚举法求解简单的古典概型问题;掌握古典概型的概率计算公式。
[课堂互动]
自学评价
1、 理解基本事件、等可能事件等概念;正确理解古典概型的特点;
3、如果某种彩票中奖的概率为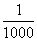 ,那么买1000张彩票一定能中奖吗?请用概率的意义解释。
,那么买1000张彩票一定能中奖吗?请用概率的意义解释。
解:不一定能中奖,因为,买1000张彩票相当于做1000次试验,因为每次试验的结果都是随机的,即每张彩票可能中奖也可能不中奖,因此,1000张彩票中可能没有一张中奖,也可能有一张、两张乃至多张中奖。
2、下表是某种油菜子在相同条件下的发芽试验结果表,请完成表格并回答题。
|
每批粒数 |
发芽的粒数 |
发芽的频率 |
|
2 |
2 |
|
|
5 |
4 |
|
|
10 |
9 |
|
|
70 |
60 |
|
|
130 |
116 |
|
|
700 |
282 |
|
|
1500 |
639 |
|
|
2000 |
1339 |
|
(1)完成上面表格:
(2)该油菜子发芽的概率约是多少?
解:(1)填入表中的数据依次为0.75,0.8,0.8,0.85,0.83,0.8,0.76.(2)由于上述频率接近0.80,因此,进球的概率约为0.80。
1、下列说法正确的是( C )
A.任一事件的概率总在(0.1)内
B.不可能事件的概率不一定为0
C.必然事件的概率一定为1
D.以上均不对
3.(1)频率的稳定性 即大量重复试验时,任何结果(事件)出现的频率尽管是随机的,却“稳定”在某一个常数附近,试验的次数越多,频率与这个常数的偏差大的可能性越小,这一常数就成为该事件的概率;
(2)“频率”和“概率”这两个概念的区别是:频率具有随机性,它反映的是某一随机事件出现的频繁程度,它反映的是随机事件出现的可能性;概率是一个客观常数,它反映了随机事件的属性.
[精典范例]
例1 某射手在同一条件下进行射击,结果如下表所示:
|
射击次数 |
击中靶心的次数 |
击中靶心的频率 |
|
10 |
8 |
|
|
20 |
19 |
|
|
50 |
44 |
|
|
100 |
92 |
|
|
200 |
178 |
|
|
500 |
455 |
|
(1)填写表中击中靶心的频率;
(2)这个射手射击一次,击中靶心的概率约是什么?
[分析]事件A出现的频数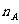 与试验次数n的比值即为事件A的频率,当事件A发生的频率fn(A)稳定在某个常数上时,这个常数即为事件A的概率。
与试验次数n的比值即为事件A的频率,当事件A发生的频率fn(A)稳定在某个常数上时,这个常数即为事件A的概率。
[解](1)表中依次填入的数据为:0.80,0.95,0.88,0.92,0.89,0.91.
(2)由于频率稳定在常数0.89,所以这个射手击一次,击中靶心的概率约是0.89。
[小结]概率实际上是频率的科学抽象,求某事件的概率可以通过求该事件的频率而得之。
例2 某人进行打靶练习,共射击10次,其中有2次中10环,有3次环中9环,有4次中8环,有1次未中靶,试计算此人中靶的概率,假设此人射击1次,试问中靶的概率约为多大?中10环的概率约为多大?
[分析]中靶的频数为9,试验次数为10,所以靶的频率为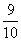 =0.9,所以中靶的概率约为0.9.
=0.9,所以中靶的概率约为0.9.
[解]此人中靶的概率约为0.9;此人射击1次,中靶的概率为0.9;中10环的概率约为0.2.
例3 在一场乒乓球比赛前,裁判员利用抽签器来决定由谁先发球,请用概率的知识解释其公平性。
[分析]这个规则是公平的,因为每个运动员先发球的概率为0.5,即每个运动员取得先发球权的概率是0.5。
[解]这个规则是公平的,因为抽签上抛后,红圈朝上与绿圈朝上的概率均是0.5,因此任何一名运动员猜中的概率都是0.5,也就是每个运动员取得先发球权的概率都是0.5。
[小结]事实上,只能使两个运动员取得先发球权的概率都是0.5的规则都是公平的。
追踪训练
2.概率的性质:
①随机事件的概率为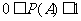 ,
,
②必然事件和不可能事件看作随机事件的两个特例,分别用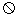 和
和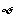 表示,必然事件的概率为
表示,必然事件的概率为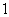 ,不可能事件的概率为
,不可能事件的概率为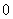 ,即
,即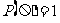 ,
,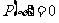 ;
;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com