
运用猜想法解题的一般步骤是:首先利用所给的递推式求出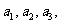 ……,然后猜想出满足递推式的一个通项公式
……,然后猜想出满足递推式的一个通项公式 ,最后用数学归纳法证明猜想是正确的。
,最后用数学归纳法证明猜想是正确的。
例13 在各项均为正数的数列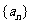 中,
中,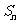 为数列
为数列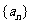 的前n项和,
的前n项和,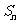 =
=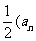 +
+ 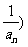 ,求其通项公式。
,求其通项公式。
4、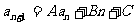 型,可化为
型,可化为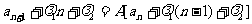 的形式。
的形式。
例12 在数列{ }中,
}中,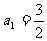 ,
, =6
=6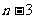 ①
①
求通项公式 .
.
解 ①式可化为:
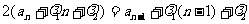 ② 比较系数可得:
② 比较系数可得:
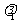 =-6,
=-6,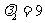 ,② 式为
,② 式为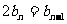
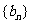 是一个等比数列,首项
是一个等比数列,首项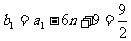 ,公比为
,公比为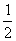 .
.
∴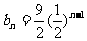
即
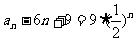
故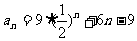 .
.
3、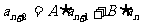 型,可化为
型,可化为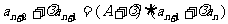 的形式。
的形式。
例11 在数列{ }中,
}中,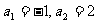 ,当
,当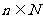 ,
,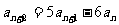 ① 求通项公式
① 求通项公式 .
.
解:①式可化为:
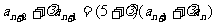
比较系数得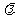 =-3或
=-3或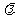 =-2,不妨取
=-2,不妨取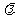 =-2.①式可化为:
=-2.①式可化为:
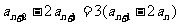
则 是一个等比数列,首项
是一个等比数列,首项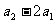 =2-2(-1)=4,公比为3.
=2-2(-1)=4,公比为3.
∴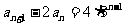 .利用上题结果有:
.利用上题结果有:
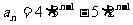 .
.
2、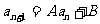
 (A、B、C为常数,下同)型,可化为
(A、B、C为常数,下同)型,可化为 =
=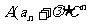 )的形式.
)的形式.
例10 在数列{ }中,
}中,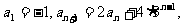 求通项公式
求通项公式 。
。
解:原递推式可化为:
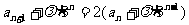 ①
①
比较系数得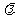 =-4,①式即是:
=-4,①式即是: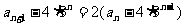 .
.
则数列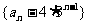 是一个等比数列,其首项
是一个等比数列,其首项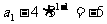 ,公比是2.
,公比是2.
∴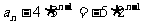
即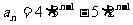 .
.
待定系数法解题的关键是从策略上规范一个递推式可变成为何种等比数列,可以少走弯路.其变换的基本形式如下:
1、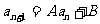 (A、B为常数)型,可化为
(A、B为常数)型,可化为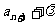 =A(
=A( )的形式.
)的形式.
例9 若数列{ }中,
}中,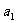 =1,
=1,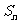 是数列{
是数列{ }的前
}的前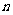 项之和,且
项之和,且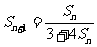 (n
(n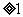 ),求数列{
),求数列{ }的通项公式是
}的通项公式是 .
.
解 递推式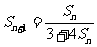 可变形为
可变形为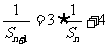 (1)
(1)
设(1)式可化为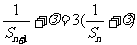 (2)
(2)
比较(1)式与(2)式的系数可得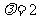 ,则有
,则有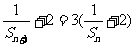 。故数列{
。故数列{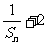 }是以
}是以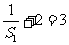 为首项,3为公比的等比数列。
为首项,3为公比的等比数列。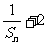 =
=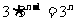 。所以
。所以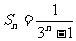 。
。
当n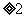 ,
,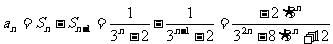 。
。
数列{ }的通项公式是
}的通项公式是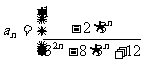
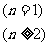 。
。
例8 若数列{ }中,
}中,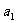 =2且
=2且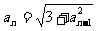 (n
(n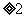 ),求它的通项公式是
),求它的通项公式是 .
.
解 将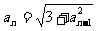 两边平方整理得
两边平方整理得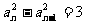 。数列{
。数列{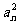 }是以
}是以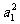 =4为首项,3为公差的等差数列。
=4为首项,3为公差的等差数列。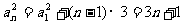 。因为
。因为 >0,所以
>0,所以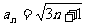 。
。
例7 若数列{ }中,
}中,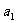 =3且
=3且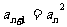 (n是正整数),则它的通项公式是
(n是正整数),则它的通项公式是 =▁▁▁(2002年上海高考题).
=▁▁▁(2002年上海高考题).
解 由题意知 >0,将
>0,将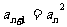 两边取对数得
两边取对数得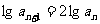 ,即
,即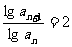 ,所以数列
,所以数列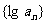 是以
是以 =
=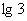 为首项,公比为2的等比数列,
为首项,公比为2的等比数列,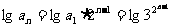 ,即
,即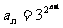 .
.
例6 已知数列{ }中,其中
}中,其中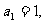 ,且当n≥2时,
,且当n≥2时,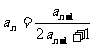 ,求通项公式
,求通项公式 。
。
解
将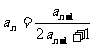 两边取倒数得:
两边取倒数得: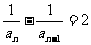 ,这说明
,这说明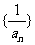 是一个等差数列,首项是
是一个等差数列,首项是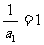 ,公差为2,所以
,公差为2,所以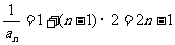 ,即
,即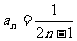 .
.
例5(1993年全国数学联赛题一试第五题)设正数列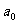 ,
,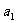 ,
, …,
…, ,…满足
,…满足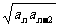
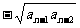 =
=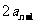
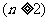 且
且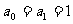 ,求
,求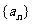 的通项公式.
的通项公式.
解 将递推式两边同除以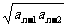 整理得:
整理得: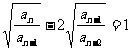
设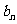 =
=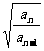 ,则
,则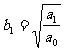 =1,
=1,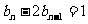 ,故有
,故有
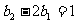 ⑴
⑴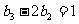 ⑵
⑵
… … … …
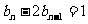 (
( )
)
由⑴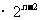 + ⑵
+ ⑵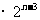 +…+(
+…+( )
)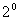 得
得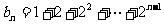 =
=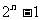 ,即
,即 =
=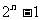 .
.
逐项相乘得: =
=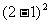
 ,考虑到
,考虑到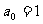 ,
,
故 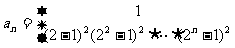
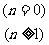 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com