5.求下列函数的极值：

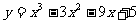(1)，　　　　(2)，[－4,4]

4.求下列函数的单调区间：

(1)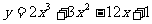　　(2)

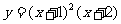
3.设函数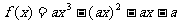在x＝1处取得极大值－2，则a＝＿＿＿＿.

2.曲线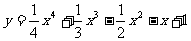的极值点是＿＿＿＿＿＿＿＿＿＿＿＿＿＿

1.若函数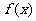在区间[a，b]内恒有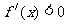，则此函数在[a，b]上的最小值是＿＿＿＿

例1.确定函数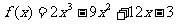的单调区间.

例2.设一质点的运动速度是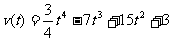，问：从t＝0到t＝10这段时间内，运动速度的改变情况怎样？

例3.求函数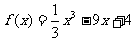的极值.

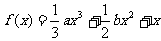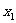例4.设函数在＝1与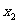＝2处取得极值，试确定a和b的值，并问此时函数在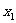与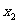处是取极大值还是极小值？

例5.求函数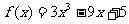在[－2,2]上的最大值和最小值.

例6.矩形横梁的强度与它断面的高的平方与宽的积成正比例，要将直径为d的圆木锯成强度最大的横梁，断面的宽和高应为多少？

例7.求内接于抛物线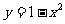与x轴所围图形内的最大矩形的面积.

例8.某种产品的总成本C(单位：万元)是产量x(单位：万件)的函数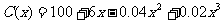：，试问：当生产水平为x＝10万件时，从降低单位成本角度看，继续提高产量是否得当？

4.设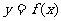是定义在[a，b]上的函数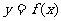，在(a，b)内有导数，可以这样求最值：

(1)求出函数在(a，b)内的可能极值点(即方程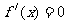在(a，b)内的根)；

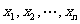(2)比较函数值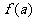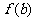，与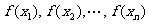，其中最大的一个为最大值，最小的一个为最小值.

3.如果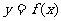在某个区间内有导数，则可以这样求它的极值：

(1)求导数＿＿＿＿＿；　　　(2)求方程＿＿＿＿＿＿＿＿的根(可能极值点)；

(3)如果在根的左侧附近为＿，右侧附近为＿，则函数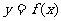在这个根处取得极＿值；如果在根的左侧附近为＿，右侧附近为＿，则函数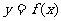在这个根处取得极＿值.

2.设函数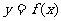在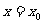及其附近有定义，如果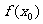的值比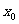附近所有各点的值都大(小)，则称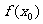是函数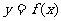的一个＿＿＿＿＿＿.

1.设函数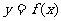在某个区间内有导数，如果在这个区间内＿＿＿＿，则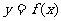是这个区间内的＿＿＿＿＿；如果在这个区间内＿＿＿，则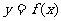是这个区间内的＿＿＿＿＿.