
例4: 求函数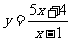 的值域。
的值域。
[分析]解析式的分子、分母都含变量,我们应设法减少变化的地方;
[解]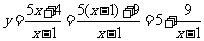 ,
,
∵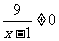 , ∴
, ∴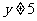 ,
,
即函数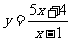 的值域为
的值域为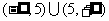 .
.
例5.求函数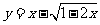 的值域。
的值域。
[解]令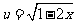 (
(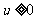 ),
),
则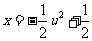 ,
,
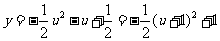 ,
,
当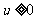 时,
时,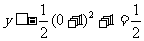 ,
,
∴函数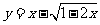 的值域为
的值域为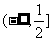 .
.
思维点拨
例4中我们减少了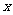 的个数后就可以求出函数的值域,该方法我们称为分离常数法,容易知道:形如
的个数后就可以求出函数的值域,该方法我们称为分离常数法,容易知道:形如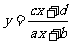
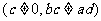 的值域为
的值域为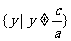 ;例5通过换元解决根号的问题我们称这种方法为换元法。
;例5通过换元解决根号的问题我们称这种方法为换元法。
追踪训练二
1.函数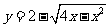 的值域为(
的值域为( 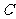 )
)
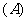
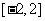
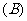
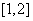
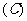
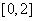
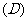
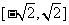
2.已知一个函数的解析式为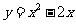 ,它的 值域为
,它的 值域为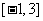 ,这样的函数有多少个?试写出其中两个函数.
,这样的函数有多少个?试写出其中两个函数.
答案:(1)5或-1。
(2)无数个,如定义域为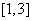 ,
,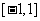 等。
等。
|
学生质疑 |
|
|
教师释疑 |
|
例4: 已知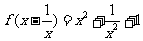 ,求函数
,求函数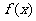 的解析式。
的解析式。
[解]
(答案: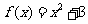 )
)
例5.已知一个函数的解析式为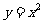 ,它的值域为
,它的值域为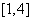 ,这样的函数有多少个?试写出其中两个函数。
,这样的函数有多少个?试写出其中两个函数。
[解]
思维点拨
解决例5这类问题,可以先写出自己熟悉的一个函数,然后再改变定义域。如本题可先写出满足条件的函数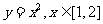 ,注意到函数图象关于
,注意到函数图象关于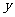 轴对称,设
轴对称,设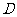 是
是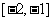 的任意一个子集,则形如
的任意一个子集,则形如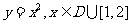 的函数都满足条件。
的函数都满足条件。
追踪训练二
1、已知a,b为常数,若f(x)=x2+4x+3,f(ax+b)=x2+10x+24,则5a-b=_________.
例4: 夏天,大家都喜欢吃西瓜,而西瓜的价格往往与西瓜的重量相关.小李到一个水果店去买西瓜,价格表上写的是:6斤以下,每斤0.4元.6斤以上9斤以下,每斤0.5元,9斤以上,每斤0.6元.此人挑了一个西瓜,称重后店主说5元1角,1角就不要了,给5元吧。可小李马上说,你不仅没少要,反而多收了我的钱。当小李讲出理由,店主只好承认了错误,照实收了钱.
同学们,你知道小李是怎样知道店主坑人的吗?其实这样的数学问题在我们身边有很多,只要你注意观察,积累,并学以致用,就能成为一个聪明人,因为数学可以使人聪明起来.
[解]若西瓜重9斤以下则最多应付4.5元,若西瓜重9斤以上,则最少也要5.4元,不可能出现5.1元这样的价钱,所以店主坑人了.
|
学生质疑 |
|
|
教师释疑 |
|
1.某电脑公司在甲乙两地各有一个分公司,甲分公司现有电脑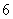 台,乙分公司现有同一型号 的电脑
台,乙分公司现有同一型号 的电脑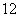 台.现
台.现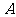 地某单位向该公司购买该型号的电脑
地某单位向该公司购买该型号的电脑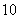 台,
台,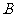 地某单位向该公司购买该型号的电脑
地某单位向该公司购买该型号的电脑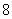 台.已知甲地运往
台.已知甲地运往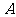 、
、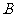 两地每台电脑的运费分别是
两地每台电脑的运费分别是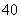 元和
元和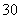 元,乙地运往
元,乙地运往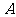 、
、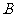 两地每台电脑的运费分别是
两地每台电脑的运费分别是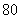 元和
元和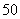 元.
元.
(1)设甲地调运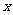 台至
台至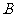 地,该公司运往
地,该公司运往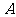 和
和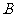 两地的总运费为
两地的总运费为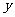 元,求
元,求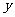 关于
关于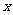 的函数关系式.
的函数关系式.
(2)若总运费不超过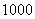 元,问能有几种调运方案?
元,问能有几种调运方案?
(3)求总运费最低的调运方案及最低运费.
分析:本题的关键在于表示出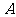 、
、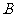 两地的电脑台数,再用函数单调性求最低运费.
两地的电脑台数,再用函数单调性求最低运费.
[解](1)设甲地调运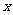 台至
台至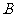 地,则剩下
地,则剩下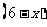 台电脑调运到
台电脑调运到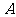 地;乙地应调运
地;乙地应调运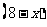 台电脑至
台电脑至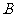 地,运往
地,运往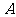 地
地
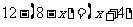 台电脑
台电脑
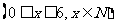 .则总运费
.则总运费
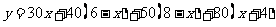
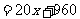 ,
,
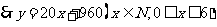 .
.
(2)若使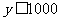 ,即
,即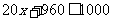 ,得
,得 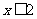
又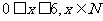 ,
,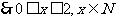
.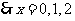 ,即能有
,即能有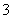 种调运方案.
种调运方案.
(3)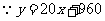 是
是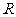 上的增函数,又
上的增函数,又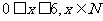 ,
,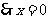 时,
时,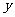 有最小值为
有最小值为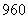 .
.
所以,从甲地运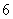 台到
台到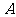 地,从乙地运
地,从乙地运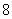 台到
台到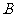 地、运
地、运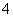 台到
台到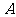 地,运费最低为
地,运费最低为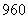 元.
元.
点评:本例题属于经费预算问题,其数学模型表现为一次函数模型求最值的问题.
3
 [师生互动]
[师生互动]
|
学生质疑 |
|
|
教师释疑 |
|
高考热点1. (2001上海,12)根据报道,我国目前已成为世界上受荒漠化危害最严重的国家之一.图2-6中(1)表示我国土地沙化总面积在上个世纪五六十年代、七八十年代、九十年代的变化情况.由图中的相关信息,可将上述有关年代中,我国年平均土地沙化面积在图1中(2)中图示为:
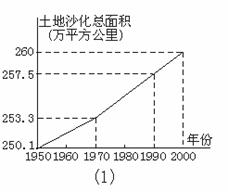
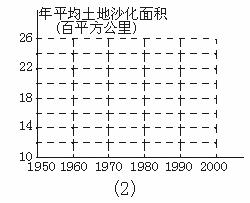
[解]如图2所示.
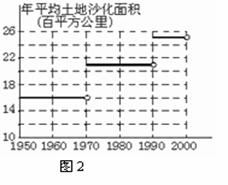
解:由图中的沙化面积可以利用 =平均面积.因为题中是分了五六十年代、六七十年代、九十年代三段.
=平均面积.因为题中是分了五六十年代、六七十年代、九十年代三段.
所以可分别求出三段的平均面积
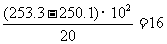
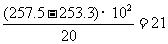 ,
,
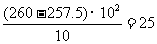
2.如图,河流航线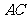 长
长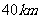 ,工厂
,工厂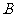 位于码头
位于码头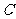 正北
正北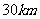 处,原来工厂
处,原来工厂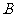 所需原料需由码头
所需原料需由码头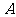 装船沿水路到码头
装船沿水路到码头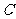 后,再改陆运到工厂
后,再改陆运到工厂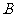 ,由于水运太长,运费颇高,工厂
,由于水运太长,运费颇高,工厂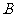 与航运局协商在
与航运局协商在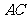 段上建一码头
段上建一码头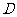 ,并由码头
,并由码头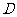 到工厂
到工厂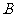 修一条新公路,原料改为按由
修一条新公路,原料改为按由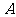 到
到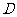 再到
再到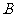 的路线运输,设
的路线运输,设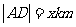
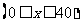 ,每
,每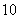 吨的货物总运费为
吨的货物总运费为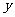 元,已知每
元,已知每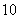 吨货物每千米运费水路为
吨货物每千米运费水路为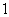 元,陆路为
元,陆路为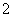 元.
元.
(1)试写出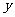 元关于
元关于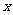 的函数关系式;
的函数关系式;
(2)要使运费最省,码头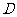 应建在何处?
应建在何处?


分析:①.总运费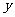 元
元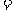 水路运费
水路运费 陆路运费
陆路运费
②.水路运费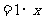 元,陆路长度
元,陆路长度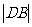
可以勾股定理求
得: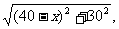
陆路运费
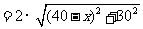 (元).
(元).
③.建立此问题的函数模型:
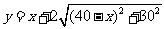
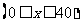 .
.
对于问题(2)我们可以利用求函数值域的方法求得运费最省时, 点的位置.
点的位置.
以上建立实际问题的函数模型均是在弄清题意的基础上,根据几何、物理等相关的知识建立的函数模型
思维点拔:
一次函数求最值主要是利用它的单调性;函数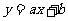 在
在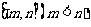 上的最值:当
上的最值:当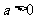 时,
时,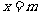 时有最小值
时有最小值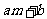 ,
,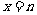 时有最大值
时有最大值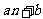 ;当
;当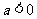 时,
时, 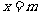 时有最大值
时有最大值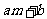 ,
,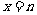 时有最小值
时有最小值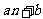
二次函数求最值也是利用它的单调性,一般都先配方.而求最值都要考虑取最值的条件.
追踪训练二
8.判断方程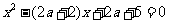 (其中
(其中 )在区间
)在区间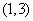 内是否有解.
内是否有解.
答案:有解.
7.求方程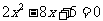 的近似解(精确到
的近似解(精确到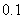 ).
).
答案: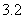 和
和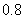
6.已知函数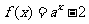 过点
过点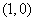 ,则方程
,则方程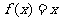 的解为
的解为 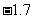 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com