
1.认识圆的标准方程并掌握推导圆的方程的思想方法;
例5:分别过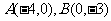 两点作两条平行线,求满足下列条件的两条直线方程:
两点作两条平行线,求满足下列条件的两条直线方程:
(1)两平行线间的距离为 ;(2)这两条直线各自绕
;(2)这两条直线各自绕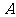 、
、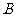 旋转,使它们之间的距离取最大值.
旋转,使它们之间的距离取最大值.
[解]
思维点拔:对称问题
|
学生质疑 |
|
|
教师释疑 |
|
在遇到对称问题时关键是分析出是属于什么对称情况,这里大致可以分为:点关与点对称,点关于直线对称,直线关于点对称,直线关于直线对称这四种情况,一旦确定为哪种情况后对应本节课的四种基本方法进行求解.
追踪训练二
1.两平行直线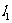 ,
,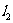 分别过
分别过 ,
,
(1)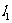 ,
,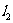 之间的距离为5,求两直线方
之间的距离为5,求两直线方
程;
(2)若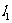 ,
,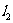 之间的距离为
之间的距离为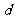 ,求
,求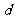 的取值范围.
的取值范围.
[解]

4.已知平行线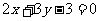 与
与
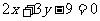 ,求与它们等距离的平行线的方程.
,求与它们等距离的平行线的方程.
|
学生质疑 |
|
|
教师释疑 |
|

3. 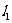 :
: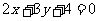 ,
, :
: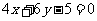
之间的距离为____________.
2. 直线 过点
过点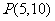 ,且与原点的距离等于
,且与原点的距离等于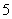 ,则直线
,则直线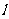 的方程为____________;
的方程为____________;
1.动点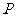 在直线
在直线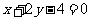 上,
上,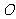 为原点,则
为原点,则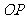 的最小值为_________;
的最小值为_________;
2. 两条平行直线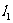 :
: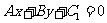 ,
, :
: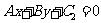 (
( )之间的距离为
)之间的距离为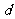 ,则______________________________.
,则______________________________.
注意:两条平行直线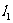 与
与 的形式必须是一般式,同时
的形式必须是一般式,同时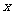 和
和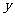 前面的系数必须化为一致.
前面的系数必须化为一致.
[精典范例]
例1:求点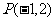 到下列直线的距离:
到下列直线的距离:
(1)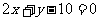 ;(2)
;(2)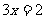 .
.
[解]
 例2:求过点
例2:求过点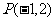 ,且与原点的距离等于
,且与原点的距离等于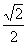 的直线方程.
的直线方程.
[解]
例3:求两条平行线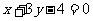 和
和
 之间的距离.
之间的距离.
分析:两条平行直线之间的距离只要在其中一条上任意取一个点,算出该点到另一直线的距离即可,从而将平行直线之间的距离转化为点到直线的距离.
[解]
例4:若直线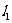 与直线
与直线
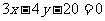 平行且距离为
平行且距离为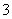 ,求直线
,求直线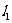 的方程.
的方程.
[解]
思维点拔:
点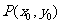 到直线
到直线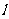 :
: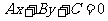 (
(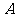 ,
,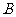 不同时为
不同时为 )
)
 的距离:
的距离: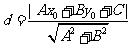 .使用该公式时应该注意:1.公式中的直线方程必须化为一般式;2.若点
.使用该公式时应该注意:1.公式中的直线方程必须化为一般式;2.若点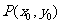 在直线
在直线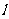 上,则
上,则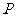 到直线
到直线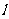 的距离为
的距离为 ,此时公式仍适用;3.特别地,点
,此时公式仍适用;3.特别地,点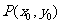 到
到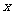 轴的距离为
轴的距离为 ,到
,到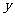 轴的距离为
轴的距离为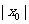 .
.
两条平行直线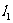 :
: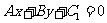 ,
, :
: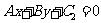 (
( )之间的距离:
)之间的距离: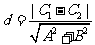 使用该公式时应该注意:
使用该公式时应该注意:
两条平行直线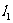 与
与 的形式必须是一般式,同时
的形式必须是一般式,同时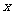 和
和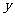 前面的系数必须化为一致.
前面的系数必须化为一致.
追踪训练一
1.点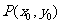 到直线
到直线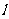 :
: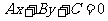 的距离:___________________________.
的距离:___________________________.
注意:
(1)公式中的直线方程必须化为一般式;
(2)分子带绝对值,分母是根式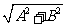 ;
;
思考:当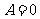 或
或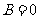 时公式成立吗?
时公式成立吗?
答:________________________________.
3.掌握两条平行直线之间的距离求法.
自学评价
2.会通过方程的思想,根据已知若干点到直线的距离大小(或关系)求点的坐标或直线的方程;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com